Performance Analysis of Photon-Limited Free-Space Optical Communications with Practical Photon-Counting Receivers
Paper and Code
Aug 24, 2024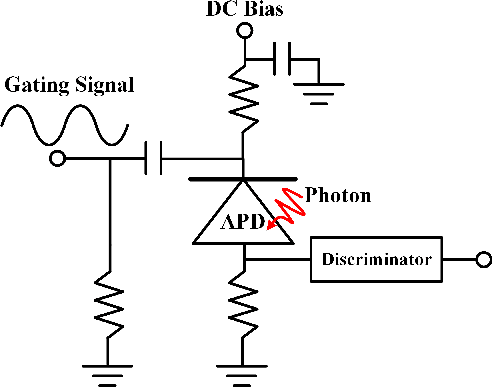
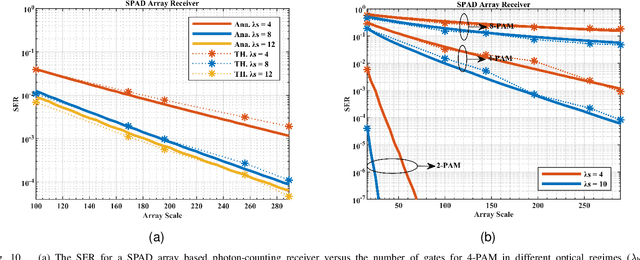
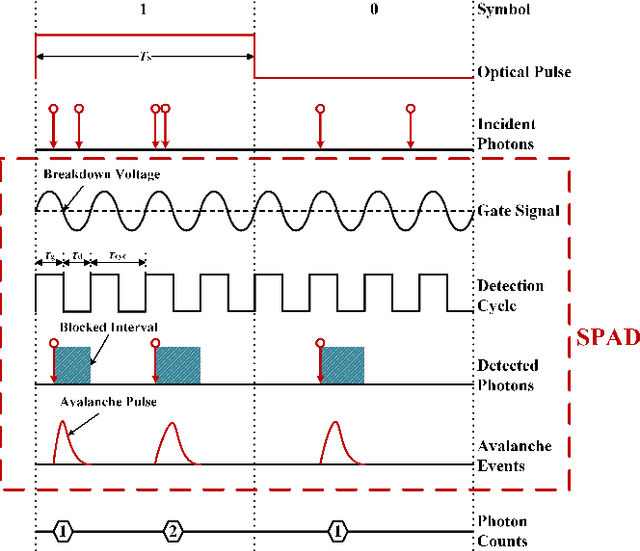
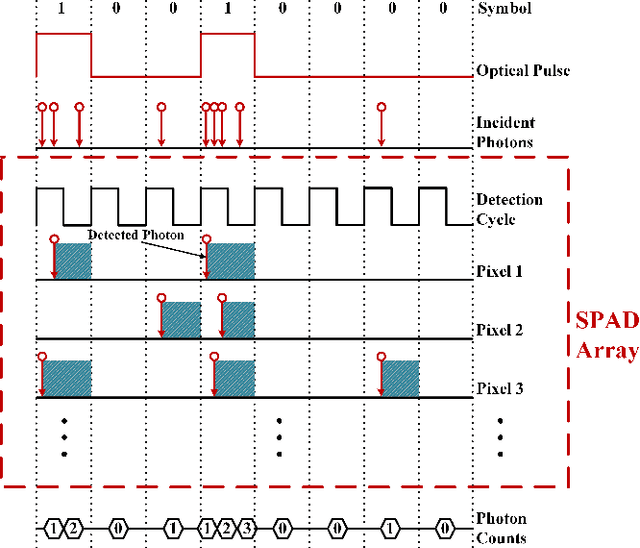
The non-perfect factors of practical photon-counting receiver are recognized as a significant challenge for long-distance photon-limited free-space optical (FSO) communication systems. This paper presents a comprehensive analytical framework for modeling the statistical properties of time-gated single-photon avalanche diode (TG-SPAD) based photon-counting receivers in presence of dead time, non-photon-number-resolving and afterpulsing effect. Drawing upon the non-Markovian characteristic of afterpulsing effect, we formulate a closed-form approximation for the probability mass function (PMF) of photon counts, when high-order pulse amplitude modulation (PAM) is used. Unlike the photon counts from a perfect photon-counting receiver, which adhere to a Poisson arrival process, the photon counts from a practical TG-SPAD based receiver are instead approximated by a binomial distribution. Additionally, by employing the maximum likelihood (ML) criterion, we derive a refined closed-form formula for determining the threshold in high-order PAM, thereby facilitating the development of an analytical model for the symbol error rate (SER). Utilizing this analytical SER model, the system performance is investigated. The numerical results underscore the crucial need to suppress background radiation below the tolerated threshold and to maintain a sufficient number of gates in order to achieve a target SER.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge