PEP: Parameter Ensembling by Perturbation

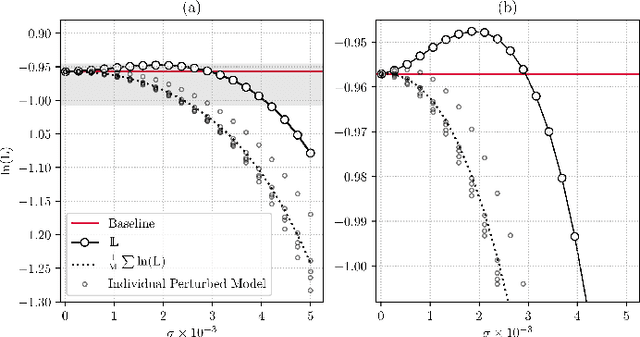
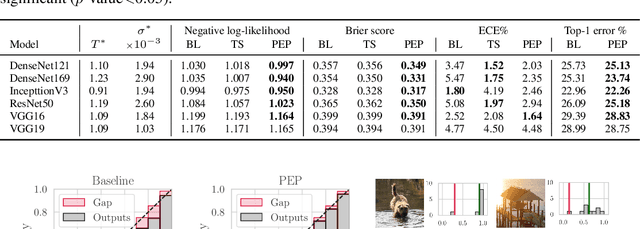
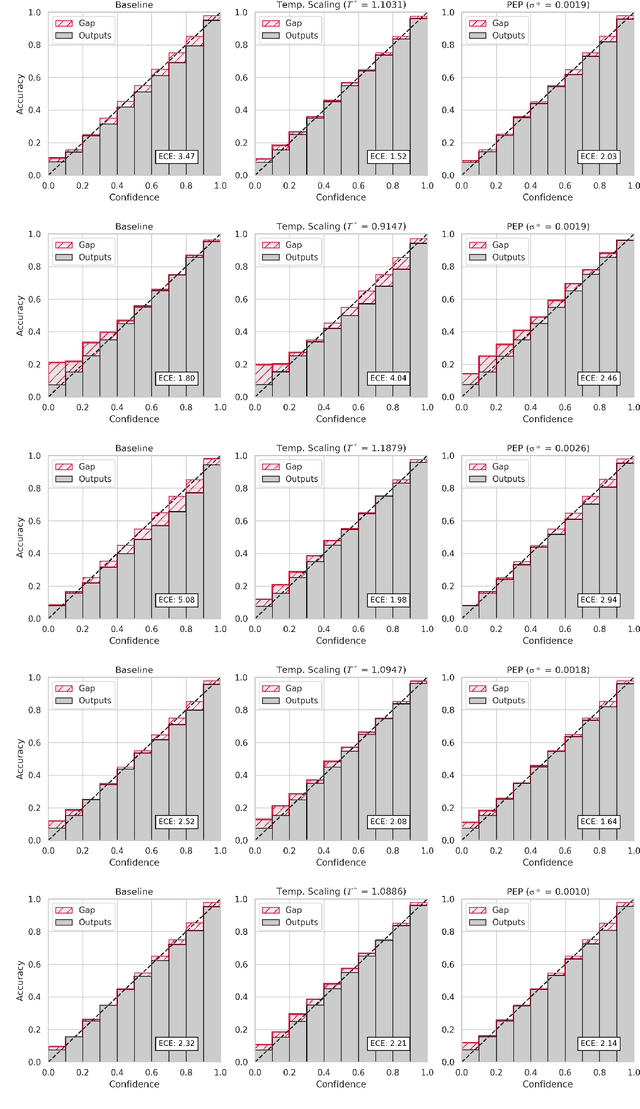
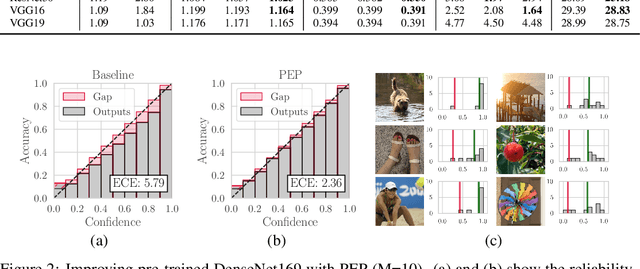
Ensembling is now recognized as an effective approach for increasing the predictive performance and calibration of deep networks. We introduce a new approach, Parameter Ensembling by Perturbation (PEP), that constructs an ensemble of parameter values as random perturbations of the optimal parameter set from training by a Gaussian with a single variance parameter. The variance is chosen to maximize the log-likelihood of the ensemble average ($\mathbb{L}$) on the validation data set. Empirically, and perhaps surprisingly, $\mathbb{L}$ has a well-defined maximum as the variance grows from zero (which corresponds to the baseline model). Conveniently, calibration level of predictions also tends to grow favorably until the peak of $\mathbb{L}$ is reached. In most experiments, PEP provides a small improvement in performance, and, in some cases, a substantial improvement in empirical calibration. We show that this "PEP effect" (the gain in log-likelihood) is related to the mean curvature of the likelihood function and the empirical Fisher information. Experiments on ImageNet pre-trained networks including ResNet, DenseNet, and Inception showed improved calibration and likelihood. We further observed a mild improvement in classification accuracy on these networks. Experiments on classification benchmarks such as MNIST and CIFAR-10 showed improved calibration and likelihood, as well as the relationship between the PEP effect and overfitting; this demonstrates that PEP can be used to probe the level of overfitting that occurred during training. In general, no special training procedure or network architecture is needed, and in the case of pre-trained networks, no additional training is needed.