Partitioned Variational Inference: A Framework for Probabilistic Federated Learning
Paper and Code
Feb 28, 2022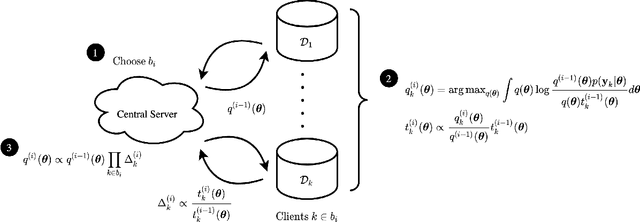
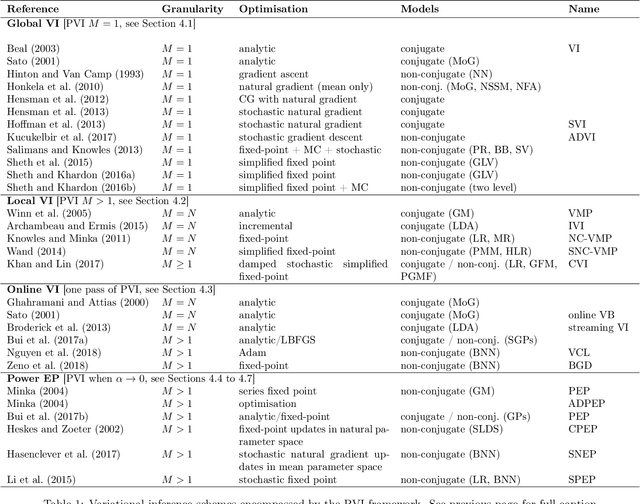
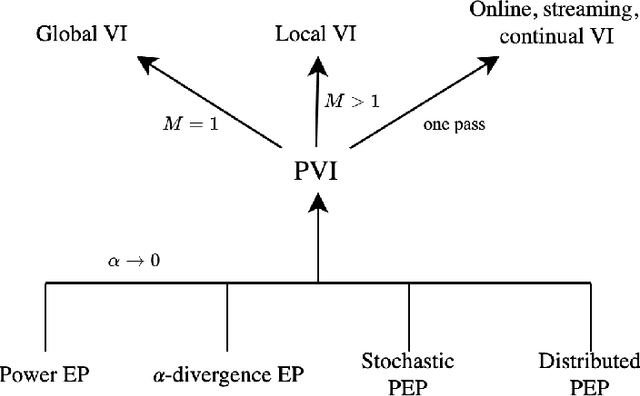
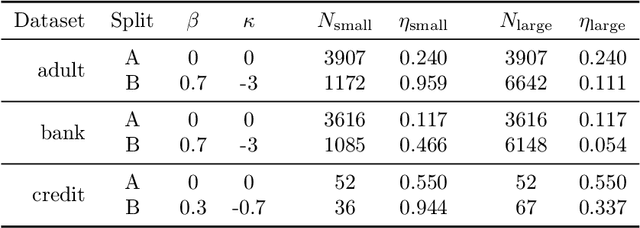
The proliferation of computing devices has brought about an opportunity to deploy machine learning models on new problem domains using previously inaccessible data. Traditional algorithms for training such models often require data to be stored on a single machine with compute performed by a single node, making them unsuitable for decentralised training on multiple devices. This deficiency has motivated the development of federated learning algorithms, which allow multiple data owners to train collaboratively and use a shared model whilst keeping local data private. However, many of these algorithms focus on obtaining point estimates of model parameters, rather than probabilistic estimates capable of capturing model uncertainty, which is essential in many applications. Variational inference (VI) has become the method of choice for fitting many modern probabilistic models. In this paper we introduce partitioned variational inference (PVI), a general framework for performing VI in the federated setting. We develop new supporting theory for PVI, demonstrating a number of properties that make it an attractive choice for practitioners; use PVI to unify a wealth of fragmented, yet related literature; and provide empirical results that showcase the effectiveness of PVI in a variety of federated settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge