MDPGT: Momentum-based Decentralized Policy Gradient Tracking
Paper and Code
Dec 06, 2021
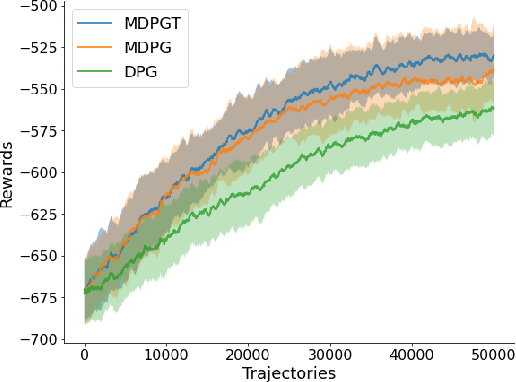
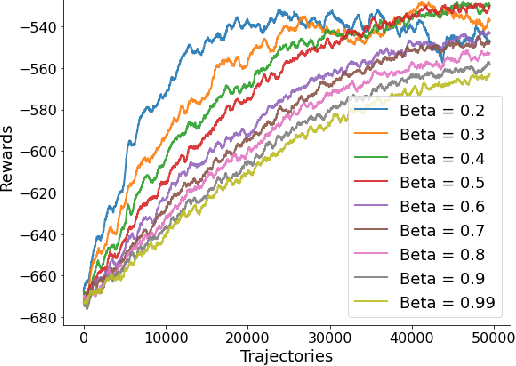
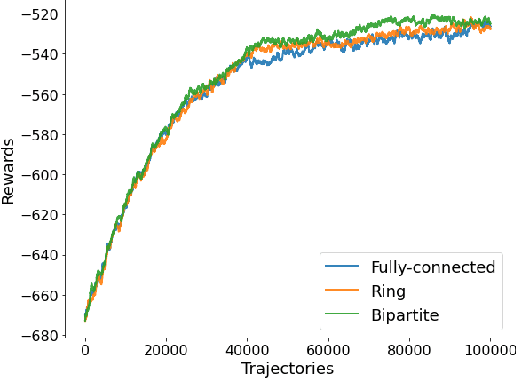
We propose a novel policy gradient method for multi-agent reinforcement learning, which leverages two different variance-reduction techniques and does not require large batches over iterations. Specifically, we propose a momentum-based decentralized policy gradient tracking (MDPGT) where a new momentum-based variance reduction technique is used to approximate the local policy gradient surrogate with importance sampling, and an intermediate parameter is adopted to track two consecutive policy gradient surrogates. Moreover, MDPGT provably achieves the best available sample complexity of $\mathcal{O}(N^{-1}\epsilon^{-3})$ for converging to an $\epsilon$-stationary point of the global average of $N$ local performance functions (possibly nonconcave). This outperforms the state-of-the-art sample complexity in decentralized model-free reinforcement learning, and when initialized with a single trajectory, the sample complexity matches those obtained by the existing decentralized policy gradient methods. We further validate the theoretical claim for the Gaussian policy function. When the required error tolerance $\epsilon$ is small enough, MDPGT leads to a linear speed up, which has been previously established in decentralized stochastic optimization, but not for reinforcement learning. Lastly, we provide empirical results on a multi-agent reinforcement learning benchmark environment to support our theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge