LOG-LIO2: A LiDAR-Inertial Odometry with Efficient Uncertainty Analysis
Paper and Code
May 02, 2024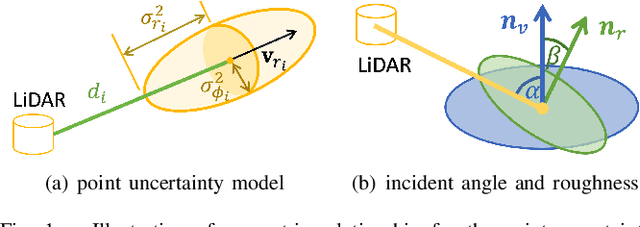
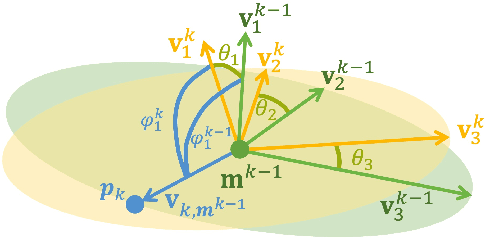
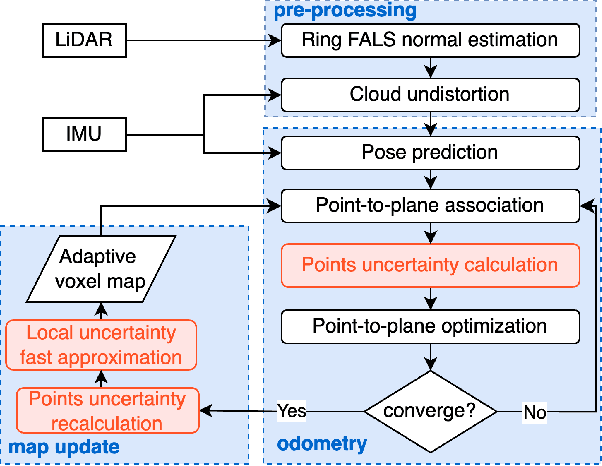
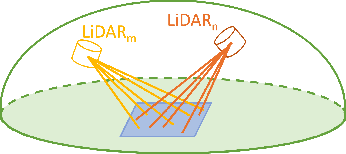
Uncertainty in LiDAR measurements, stemming from factors such as range sensing, is crucial for LIO (LiDAR-Inertial Odometry) systems as it affects the accurate weighting in the loss function. While recent LIO systems address uncertainty related to range sensing, the impact of incident angle on uncertainty is often overlooked by the community. Moreover, the existing uncertainty propagation methods suffer from computational inefficiency. This paper proposes a comprehensive point uncertainty model that accounts for both the uncertainties from LiDAR measurements and surface characteristics, along with an efficient local uncertainty analytical method for LiDAR-based state estimation problem. We employ a projection operator that separates the uncertainty into the ray direction and its orthogonal plane. Then, we derive incremental Jacobian matrices of eigenvalues and eigenvectors w.r.t. points, which enables a fast approximation of uncertainty propagation. This approach eliminates the requirement for redundant traversal of points, significantly reducing the time complexity of uncertainty propagation from $\mathcal{O} (n)$ to $\mathcal{O} (1)$ when a new point is added. Simulations and experiments on public datasets are conducted to validate the accuracy and efficiency of our formulations. The proposed methods have been integrated into a LIO system, which is available at https://github.com/tiev-tongji/LOG-LIO2.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge