Learning to Identify Top Elo Ratings: A Dueling Bandits Approach
Paper and Code
Jan 20, 2022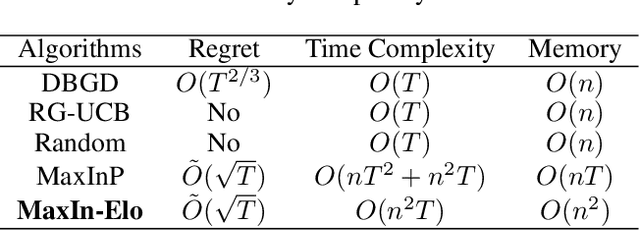
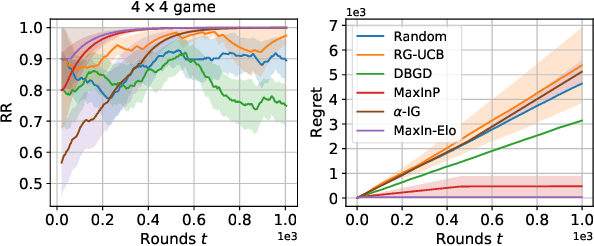
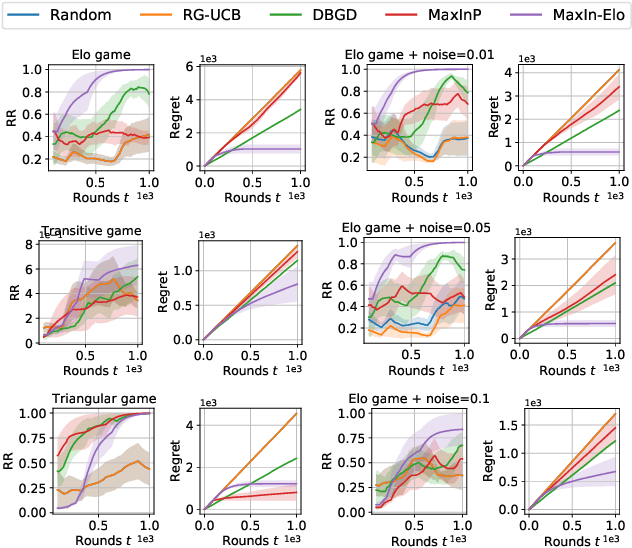

The Elo rating system is widely adopted to evaluate the skills of (chess) game and sports players. Recently it has been also integrated into machine learning algorithms in evaluating the performance of computerised AI agents. However, an accurate estimation of the Elo rating (for the top players) often requires many rounds of competitions, which can be expensive to carry out. In this paper, to improve the sample efficiency of the Elo evaluation (for top players), we propose an efficient online match scheduling algorithm. Specifically, we identify and match the top players through a dueling bandits framework and tailor the bandit algorithm to the gradient-based update of Elo. We show that it reduces the per-step memory and time complexity to constant, compared to the traditional likelihood maximization approaches requiring $O(t)$ time. Our algorithm has a regret guarantee of $\tilde{O}(\sqrt{T})$, sublinear in the number of competition rounds and has been extended to the multidimensional Elo ratings for handling intransitive games. We empirically demonstrate that our method achieves superior convergence speed and time efficiency on a variety of gaming tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge