Learning Robust and Lightweight Model through Separable Structured Transformations
Paper and Code
Dec 29, 2021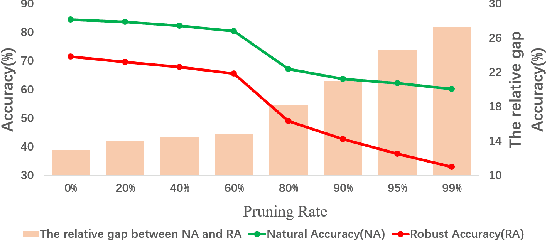

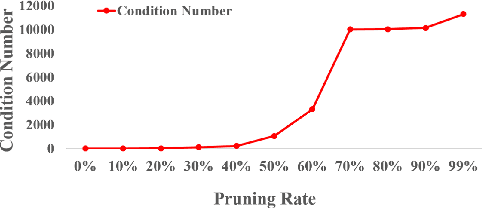
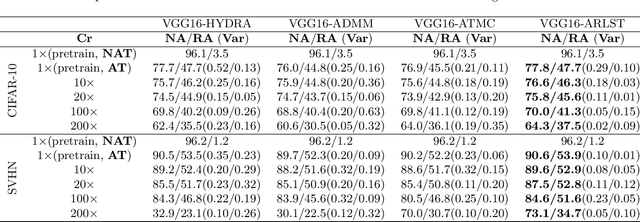
With the proliferation of mobile devices and the Internet of Things, deep learning models are increasingly deployed on devices with limited computing resources and memory, and are exposed to the threat of adversarial noise. Learning deep models with both lightweight and robustness is necessary for these equipments. However, current deep learning solutions are difficult to learn a model that possesses these two properties without degrading one or the other. As is well known, the fully-connected layers contribute most of the parameters of convolutional neural networks. We perform a separable structural transformation of the fully-connected layer to reduce the parameters, where the large-scale weight matrix of the fully-connected layer is decoupled by the tensor product of several separable small-sized matrices. Note that data, such as images, no longer need to be flattened before being fed to the fully-connected layer, retaining the valuable spatial geometric information of the data. Moreover, in order to further enhance both lightweight and robustness, we propose a joint constraint of sparsity and differentiable condition number, which is imposed on these separable matrices. We evaluate the proposed approach on MLP, VGG-16 and Vision Transformer. The experimental results on datasets such as ImageNet, SVHN, CIFAR-100 and CIFAR10 show that we successfully reduce the amount of network parameters by 90%, while the robust accuracy loss is less than 1.5%, which is better than the SOTA methods based on the original fully-connected layer. Interestingly, it can achieve an overwhelming advantage even at a high compression rate, e.g., 200 times.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge