Learned Cone-Beam CT Reconstruction Using Neural Ordinary Differential Equations
Paper and Code
Jan 19, 2022
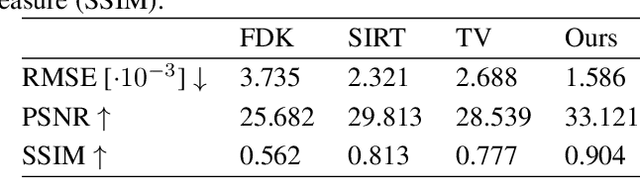

Learned iterative reconstruction algorithms for inverse problems offer the flexibility to combine analytical knowledge about the problem with modules learned from data. This way, they achieve high reconstruction performance while ensuring consistency with the measured data. In computed tomography, extending such approaches from 2D fan-beam to 3D cone-beam data is challenging due to the prohibitively high GPU memory that would be needed to train such models. This paper proposes to use neural ordinary differential equations to solve the reconstruction problem in a residual formulation via numerical integration. For training, there is no need to backpropagate through several unrolled network blocks nor through the internals of the solver. Instead, the gradients are obtained very memory-efficiently in the neural ODE setting allowing for training on a single consumer graphics card. The method is able to reduce the root mean squared error by over 30% compared to the best performing classical iterative reconstruction algorithm and produces high quality cone-beam reconstructions even in a sparse view scenario.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge