Latent Constrained Correlation Filters for Object Localization
Paper and Code
Jun 03, 2017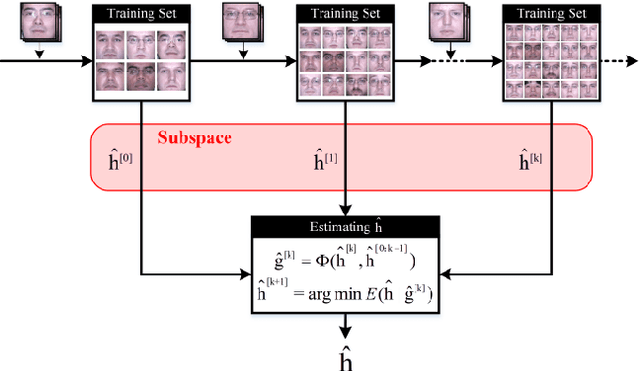
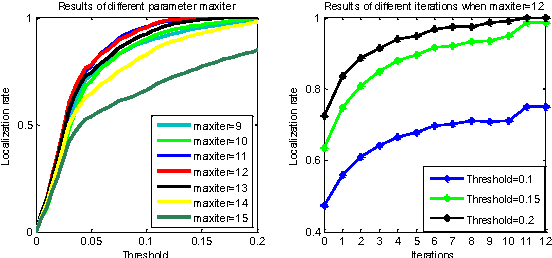
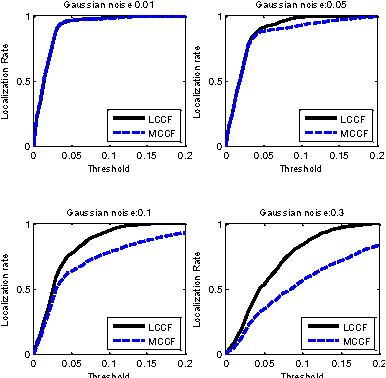
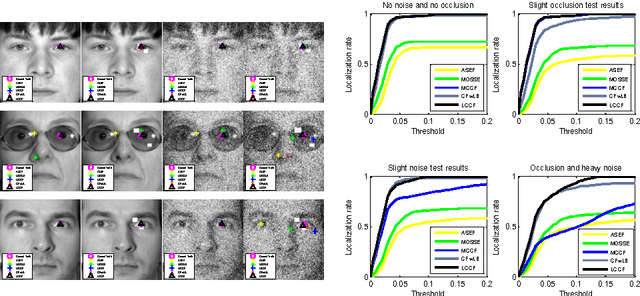
There is a neglected fact in the traditional machine learning methods that the data sampling can actually lead to the solution sampling. We consider this observation to be important because having the solution sampling available makes the variable distribution estimation, which is a problem in many learning-related applications, more tractable. In this paper, we implement this idea on correlation filter, which has attracted much attention in the past few years due to its high performance with a low computational cost. More specifically, we propose a new method, named latent constrained correlation filters (LCCF) by mapping the correlation filters to a given latent subspace, in which we establish a new learning framework that embeds distribution-related constraints into the original problem. We further introduce a subspace based alternating direction method of multipliers (SADMM) to efficiently solve the optimization problem, which is proved to converge at the saddle point. Our approach is successfully applied to two different tasks inclduing eye localization and car detection. Extensive experiments demonstrate that LCCF outperforms the state-of-the-art methods when samples are suffered from noise and occlusion.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge