Joint Graph Decomposition and Node Labeling: Problem, Algorithms, Applications
Paper and Code
Feb 21, 2017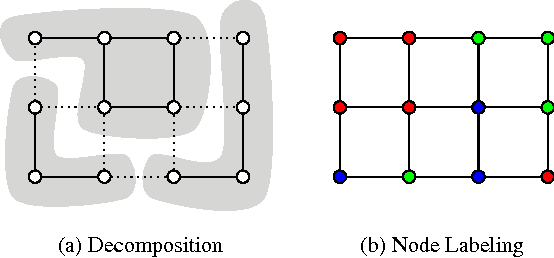
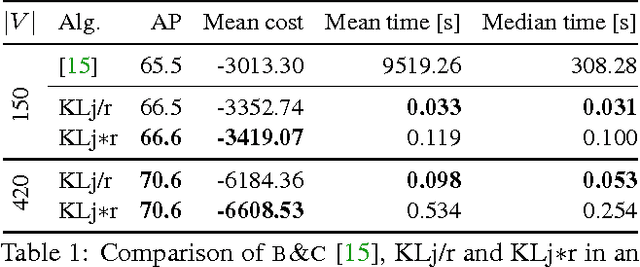
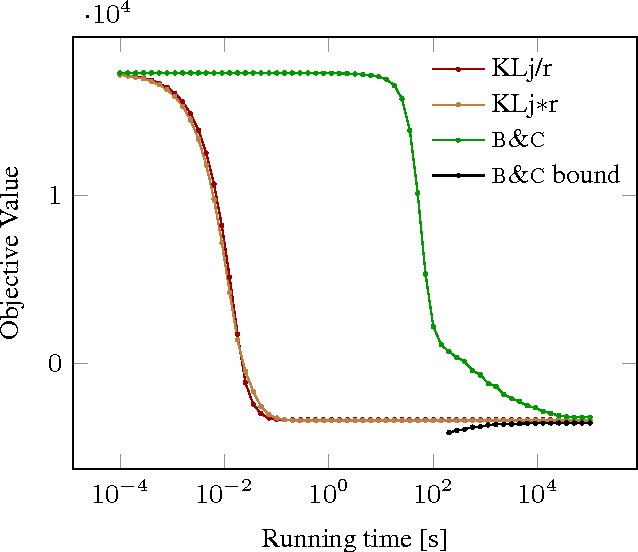
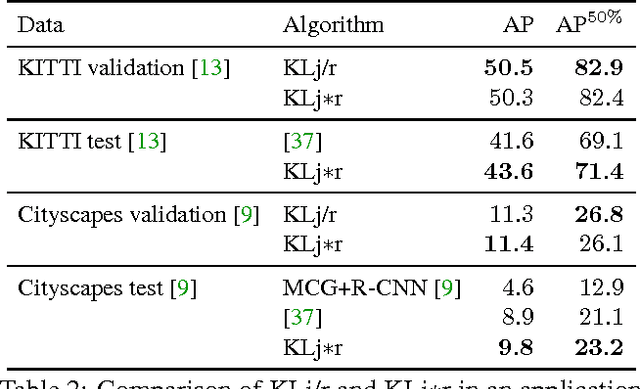
We state a combinatorial optimization problem whose feasible solutions define both a decomposition and a node labeling of a given graph. This problem offers a common mathematical abstraction of seemingly unrelated computer vision tasks, including instance-separating semantic segmentation, articulated human body pose estimation and multiple object tracking. Conceptually, the problem we state generalizes the unconstrained integer quadratic program and the minimum cost lifted multicut problem, both of which are NP-hard. In order to find feasible solutions efficiently, we define two local search algorithms that converge monotonously to a local optimum, offering a feasible solution at any time. To demonstrate their effectiveness in tackling computer vision tasks, we apply these algorithms to instances of the problem that we construct from published data, using published algorithms. We report state-of-the-art application-specific accuracy for the three above-mentioned applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge