Iterated Support Vector Machines for Distance Metric Learning
Paper and Code
Feb 02, 2015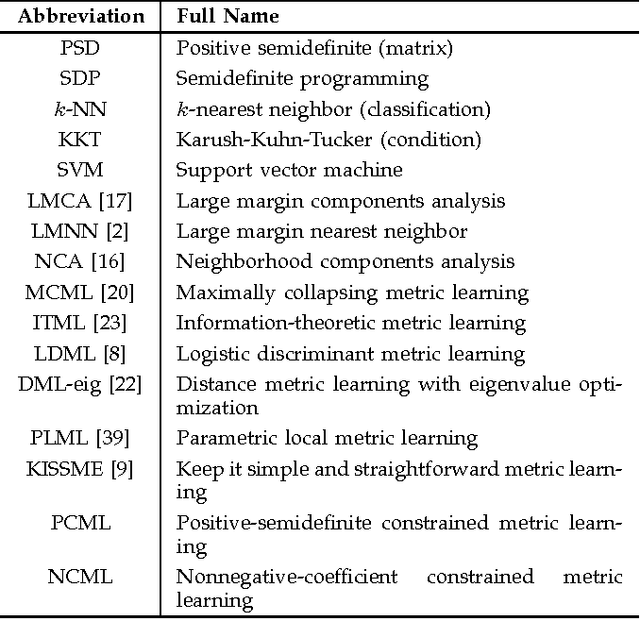
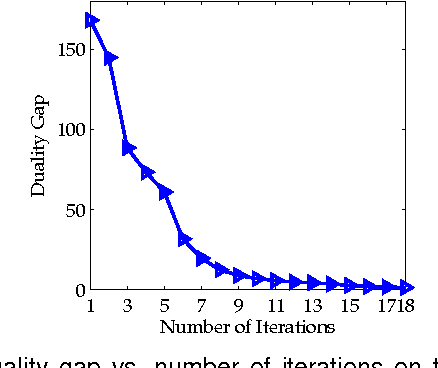
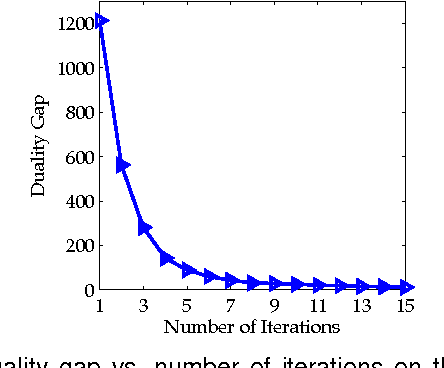
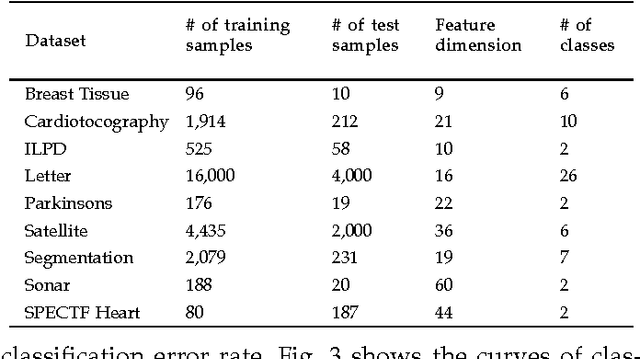
Distance metric learning aims to learn from the given training data a valid distance metric, with which the similarity between data samples can be more effectively evaluated for classification. Metric learning is often formulated as a convex or nonconvex optimization problem, while many existing metric learning algorithms become inefficient for large scale problems. In this paper, we formulate metric learning as a kernel classification problem, and solve it by iterated training of support vector machines (SVM). The new formulation is easy to implement, efficient in training, and tractable for large-scale problems. Two novel metric learning models, namely Positive-semidefinite Constrained Metric Learning (PCML) and Nonnegative-coefficient Constrained Metric Learning (NCML), are developed. Both PCML and NCML can guarantee the global optimality of their solutions. Experimental results on UCI dataset classification, handwritten digit recognition, face verification and person re-identification demonstrate that the proposed metric learning methods achieve higher classification accuracy than state-of-the-art methods and they are significantly more efficient in training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge