Inductive Representation Learning in Large Attributed Graphs
Paper and Code
Nov 22, 2017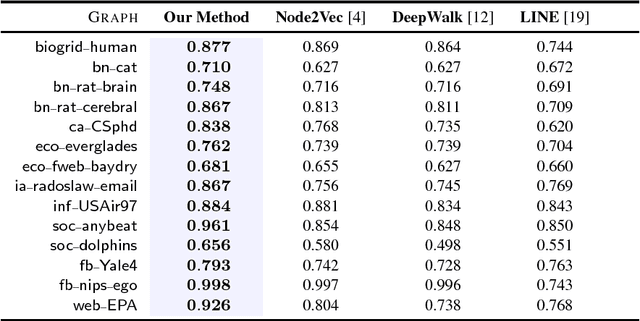
Graphs (networks) are ubiquitous and allow us to model entities (nodes) and the dependencies (edges) between them. Learning a useful feature representation from graph data lies at the heart and success of many machine learning tasks such as classification, anomaly detection, link prediction, among many others. Many existing techniques use random walks as a basis for learning features or estimating the parameters of a graph model for a downstream prediction task. Examples include recent node embedding methods such as DeepWalk, node2vec, as well as graph-based deep learning algorithms. However, the simple random walk used by these methods is fundamentally tied to the identity of the node. This has three main disadvantages. First, these approaches are inherently transductive and do not generalize to unseen nodes and other graphs. Second, they are not space-efficient as a feature vector is learned for each node which is impractical for large graphs. Third, most of these approaches lack support for attributed graphs. To make these methods more generally applicable, we propose a framework for inductive network representation learning based on the notion of attributed random walk that is not tied to node identity and is instead based on learning a function $\Phi : \mathrm{\rm \bf x} \rightarrow w$ that maps a node attribute vector $\mathrm{\rm \bf x}$ to a type $w$. This framework serves as a basis for generalizing existing methods such as DeepWalk, node2vec, and many other previous methods that leverage traditional random walks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge