Incorporating Rich Social Interactions Into MDPs
Paper and Code
Oct 22, 2021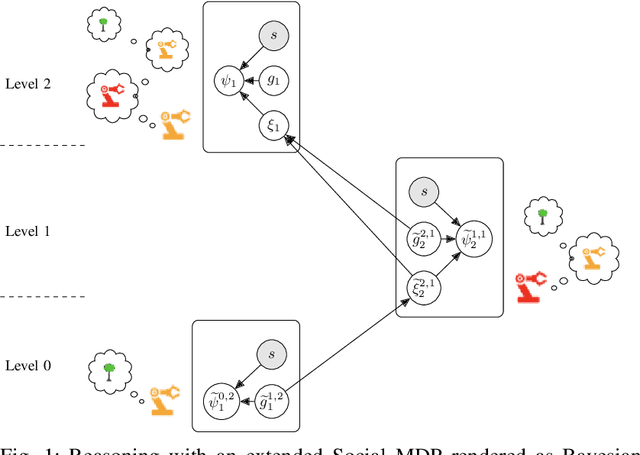

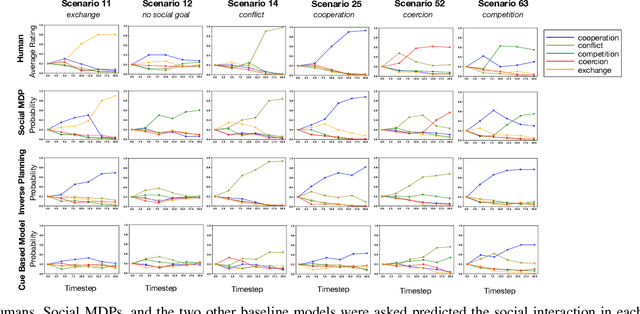

Much of what we do as humans is engage socially with other agents, a skill that robots must also eventually possess. We demonstrate that a rich theory of social interactions originating from microsociology and economics can be formalized by extending a nested MDP where agents reason about arbitrary functions of each other's hidden rewards. This extended Social MDP allows us to encode the five basic interactions that underlie microsociology: cooperation, conflict, coercion, competition, and exchange. The result is a robotic agent capable of executing social interactions zero-shot in new environments; like humans it can engage socially in novel ways even without a single example of that social interaction. Moreover, the judgments of these Social MDPs align closely with those of humans when considering which social interaction is taking place in an environment. This method both sheds light on the nature of social interactions, by providing concrete mathematical definitions, and brings rich social interactions into a mathematical framework that has proven to be natural for robotics, MDPs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge