HyperNeRF: A Higher-Dimensional Representation for Topologically Varying Neural Radiance Fields

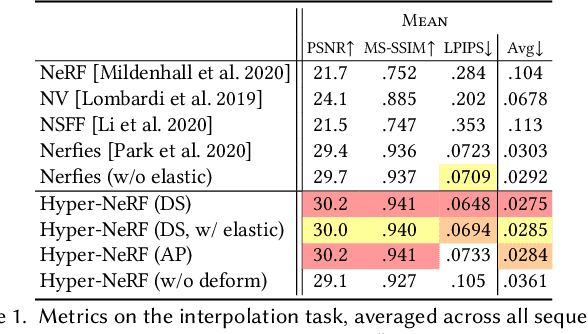
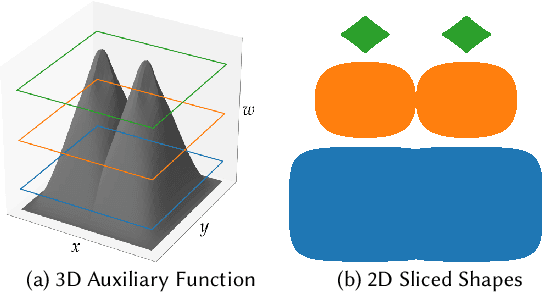
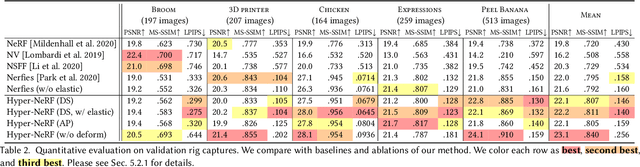
Neural Radiance Fields (NeRF) are able to reconstruct scenes with unprecedented fidelity, and various recent works have extended NeRF to handle dynamic scenes. A common approach to reconstruct such non-rigid scenes is through the use of a learned deformation field mapping from coordinates in each input image into a canonical template coordinate space. However, these deformation-based approaches struggle to model changes in topology, as topological changes require a discontinuity in the deformation field, but these deformation fields are necessarily continuous. We address this limitation by lifting NeRFs into a higher dimensional space, and by representing the 5D radiance field corresponding to each individual input image as a slice through this "hyper-space". Our method is inspired by level set methods, which model the evolution of surfaces as slices through a higher dimensional surface. We evaluate our method on two tasks: (i) interpolating smoothly between "moments", i.e., configurations of the scene, seen in the input images while maintaining visual plausibility, and (ii) novel-view synthesis at fixed moments. We show that our method, which we dub HyperNeRF, outperforms existing methods on both tasks by significant margins. Compared to Nerfies, HyperNeRF reduces average error rates by 8.6% for interpolation and 8.8% for novel-view synthesis, as measured by LPIPS.