Hierarchical Invariance for Robust and Interpretable Vision Tasks at Larger Scales

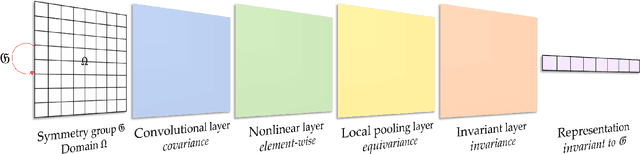
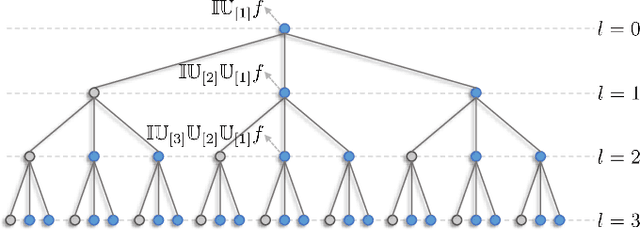
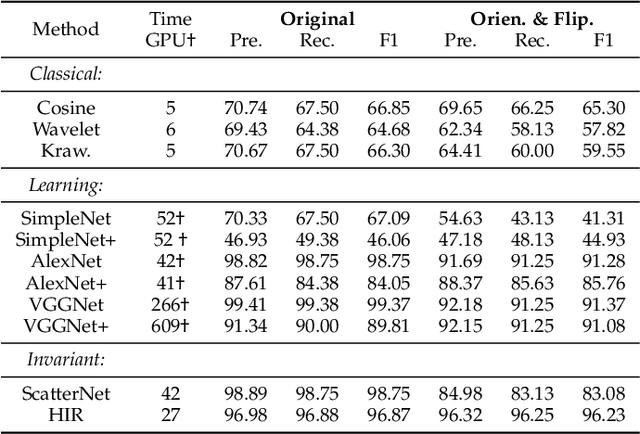
Developing robust and interpretable vision systems is a crucial step towards trustworthy artificial intelligence. In this regard, a promising paradigm considers embedding task-required invariant structures, e.g., geometric invariance, in the fundamental image representation. However, such invariant representations typically exhibit limited discriminability, limiting their applications in larger-scale trustworthy vision tasks. For this open problem, we conduct a systematic investigation of hierarchical invariance, exploring this topic from theoretical, practical, and application perspectives. At the theoretical level, we show how to construct over-complete invariants with a Convolutional Neural Networks (CNN)-like hierarchical architecture yet in a fully interpretable manner. The general blueprint, specific definitions, invariant properties, and numerical implementations are provided. At the practical level, we discuss how to customize this theoretical framework into a given task. With the over-completeness, discriminative features w.r.t. the task can be adaptively formed in a Neural Architecture Search (NAS)-like manner. We demonstrate the above arguments with accuracy, invariance, and efficiency results on texture, digit, and parasite classification experiments. Furthermore, at the application level, our representations are explored in real-world forensics tasks on adversarial perturbations and Artificial Intelligence Generated Content (AIGC). Such applications reveal that the proposed strategy not only realizes the theoretically promised invariance, but also exhibits competitive discriminability even in the era of deep learning. For robust and interpretable vision tasks at larger scales, hierarchical invariant representation can be considered as an effective alternative to traditional CNN and invariants.