Graph Edge Representation via Tensor Product Graph Convolutional Representation
Paper and Code
Jun 21, 2024


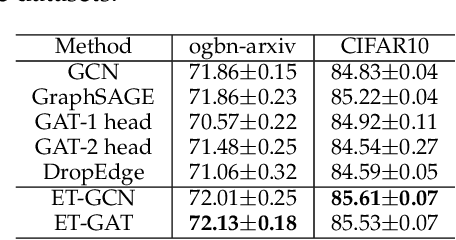
Graph Convolutional Networks (GCNs) have been widely studied. The core of GCNs is the definition of convolution operators on graphs. However, existing Graph Convolution (GC) operators are mainly defined on adjacency matrix and node features and generally focus on obtaining effective node embeddings which cannot be utilized to address the graphs with (high-dimensional) edge features. To address this problem, by leveraging tensor contraction representation and tensor product graph diffusion theories, this paper analogously defines an effective convolution operator on graphs with edge features which is named as Tensor Product Graph Convolution (TPGC). The proposed TPGC aims to obtain effective edge embeddings. It provides a complementary model to traditional graph convolutions (GCs) to address the more general graph data analysis with both node and edge features. Experimental results on several graph learning tasks demonstrate the effectiveness of the proposed TPGC.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge