Globally Variance-Constrained Sparse Representation and Its Application in Image Set Coding
Paper and Code
May 03, 2018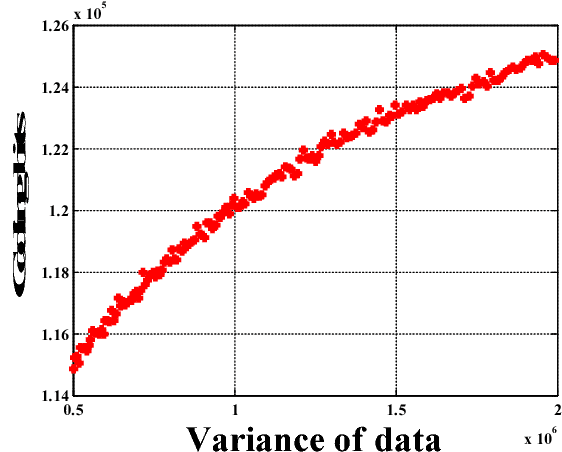

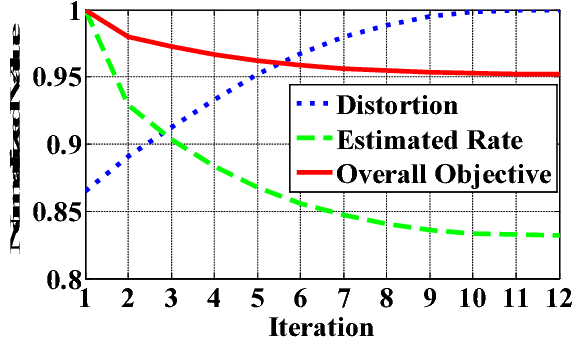
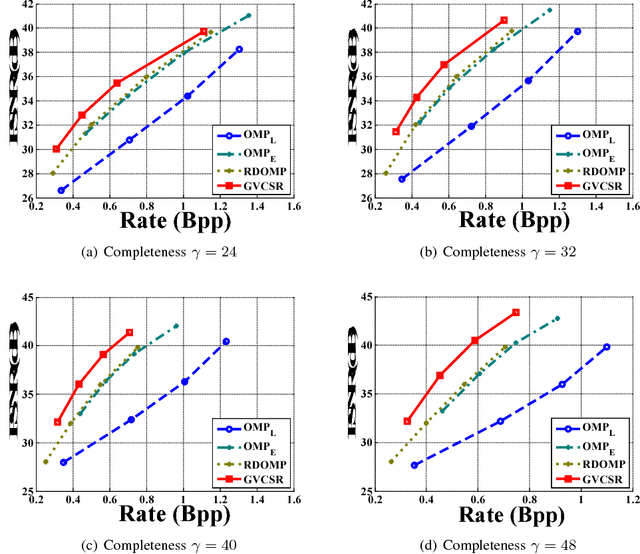
Sparse representation leads to an efficient way to approximately recover a signal by the linear composition of a few bases from a learnt dictionary, based on which various successful applications have been achieved. However, in the scenario of data compression, its efficiency and popularity are hindered. It is because of the fact that encoding sparsely distributed coefficients may consume more bits for representing the index of nonzero coefficients. Therefore, introducing an accurate rate-constraint in sparse coding and dictionary learning becomes meaningful, which has not been fully exploited in the context of sparse representation. According to the Shannon entropy inequality, the variance of a Gaussian distributed data bounds its entropy, indicating the actual bitrate can be well estimated by its variance. Hence, a Globally Variance-Constrained Sparse Representation (GVCSR) model is proposed in this work, where a variance-constrained rate term is introduced to the optimization process. Specifically, we employ the Alternating Direction Method of Multipliers (ADMM) to solve the non-convex optimization problem for sparse coding and dictionary learning, both of them have shown the state-of-the-art rate-distortion performance for image representation. Furthermore, we investigate the potential of applying the GVCSR algorithm in the practical image set compression, where the optimized dictionary is trained to efficiently represent the images captured in similar scenarios by implicitly utilizing inter-image correlations. Experimental results have demonstrated superior rate-distortion performance against the state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge