Givens Coordinate Descent Methods for Rotation Matrix Learning in Trainable Embedding Indexes
Paper and Code
Mar 09, 2022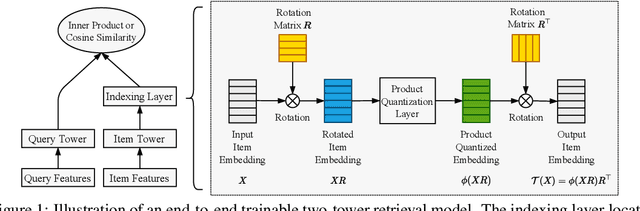
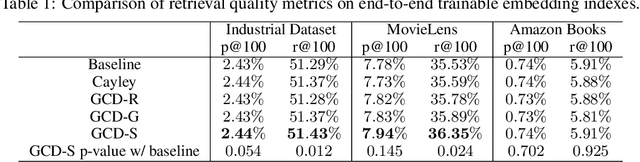
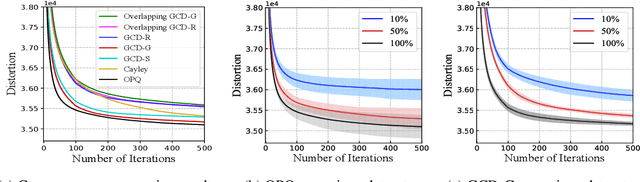
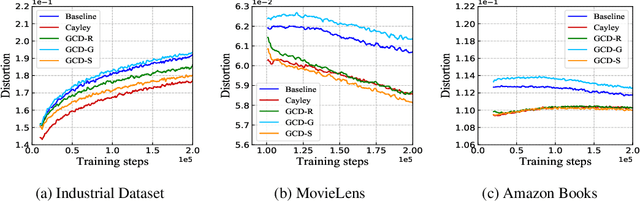
Product quantization (PQ) coupled with a space rotation, is widely used in modern approximate nearest neighbor (ANN) search systems to significantly compress the disk storage for embeddings and speed up the inner product computation. Existing rotation learning methods, however, minimize quantization distortion for fixed embeddings, which are not applicable to an end-to-end training scenario where embeddings are updated constantly. In this paper, based on geometric intuitions from Lie group theory, in particular the special orthogonal group $SO(n)$, we propose a family of block Givens coordinate descent algorithms to learn rotation matrix that are provably convergent on any convex objectives. Compared to the state-of-the-art SVD method, the Givens algorithms are much more parallelizable, reducing runtime by orders of magnitude on modern GPUs, and converge more stably according to experimental studies. They further improve upon vanilla product quantization significantly in an end-to-end training scenario.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge