Geometry-aware Bayesian Optimization in Robotics using Riemannian Matérn Kernels
Paper and Code
Nov 02, 2021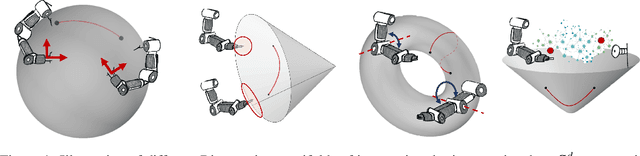


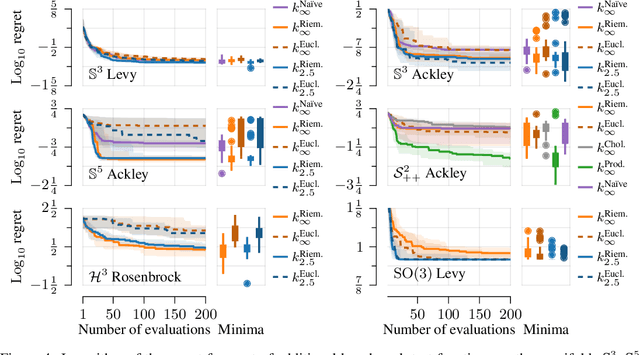
Bayesian optimization is a data-efficient technique which can be used for control parameter tuning, parametric policy adaptation, and structure design in robotics. Many of these problems require optimization of functions defined on non-Euclidean domains like spheres, rotation groups, or spaces of positive-definite matrices. To do so, one must place a Gaussian process prior, or equivalently define a kernel, on the space of interest. Effective kernels typically reflect the geometry of the spaces they are defined on, but designing them is generally non-trivial. Recent work on the Riemannian Mat\'ern kernels, based on stochastic partial differential equations and spectral theory of the Laplace-Beltrami operator, offers promising avenues towards constructing such geometry-aware kernels. In this paper, we study techniques for implementing these kernels on manifolds of interest in robotics, demonstrate their performance on a set of artificial benchmark functions, and illustrate geometry-aware Bayesian optimization for a variety of robotic applications, covering orientation control, manipulability optimization, and motion planning, while showing its improved performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge