FiLM: Frequency improved Legendre Memory Model for Long-term Time Series Forecasting
Paper and Code
May 24, 2022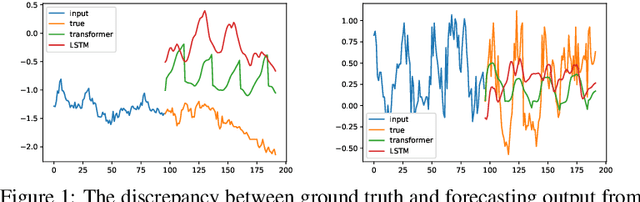

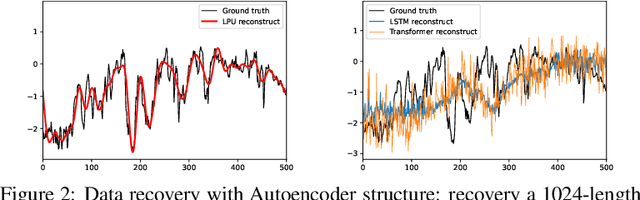

Recent studies have shown that deep learning models such as RNNs and Transformers have brought significant performance gains for long-term forecasting of time series because they effectively utilize historical information. We found, however, that there is still great room for improvement in how to preserve historical information in neural networks while avoiding overfitting to noise presented in the history. Addressing this allows better utilization of the capabilities of deep learning models. To this end, we design a \textbf{F}requency \textbf{i}mproved \textbf{L}egendre \textbf{M}emory model, or {\bf FiLM}: it applies Legendre Polynomials projections to approximate historical information, uses Fourier projection to remove noise, and adds a low-rank approximation to speed up computation. Our empirical studies show that the proposed FiLM significantly improves the accuracy of state-of-the-art models in multivariate and univariate long-term forecasting by (\textbf{20.3\%}, \textbf{22.6\%}), respectively. We also demonstrate that the representation module developed in this work can be used as a general plug-in to improve the long-term prediction performance of other deep learning modules. Code will be released soon.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge