Fast Conditional Network Compression Using Bayesian HyperNetworks
Paper and Code
May 13, 2022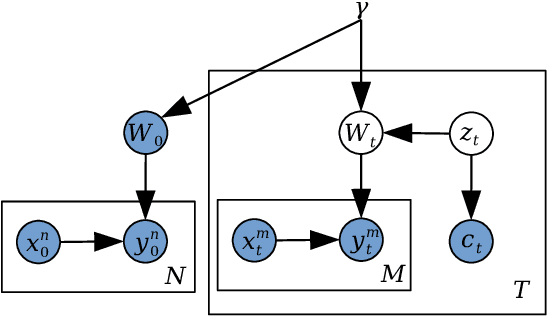
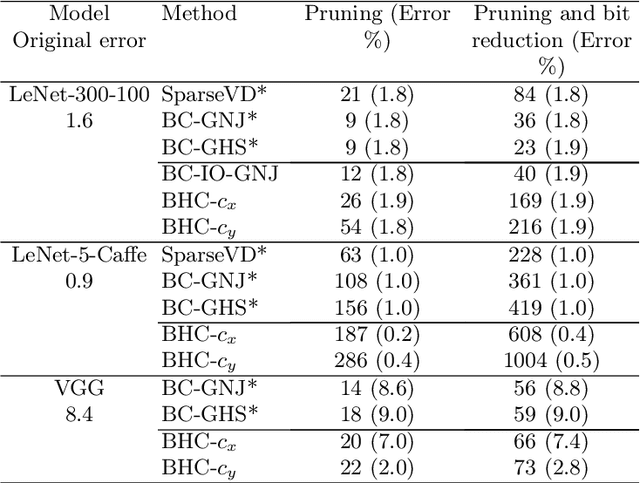
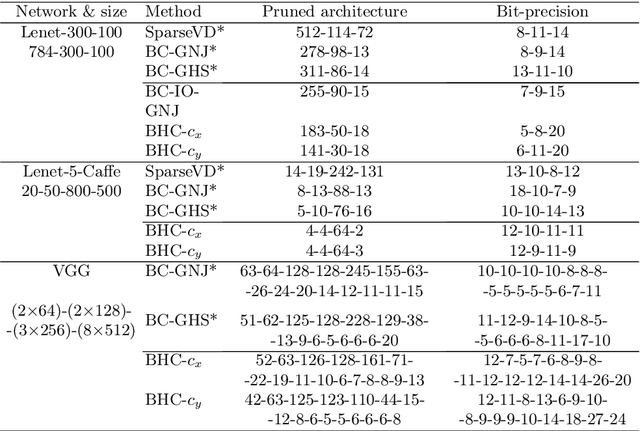
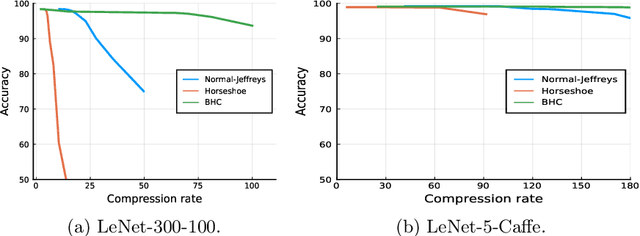
We introduce a conditional compression problem and propose a fast framework for tackling it. The problem is how to quickly compress a pretrained large neural network into optimal smaller networks given target contexts, e.g. a context involving only a subset of classes or a context where only limited compute resource is available. To solve this, we propose an efficient Bayesian framework to compress a given large network into much smaller size tailored to meet each contextual requirement. We employ a hypernetwork to parameterize the posterior distribution of weights given conditional inputs and minimize a variational objective of this Bayesian neural network. To further reduce the network sizes, we propose a new input-output group sparsity factorization of weights to encourage more sparseness in the generated weights. Our methods can quickly generate compressed networks with significantly smaller sizes than baseline methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge