Estimating informativeness of samples with Smooth Unique Information
Paper and Code
Jan 17, 2021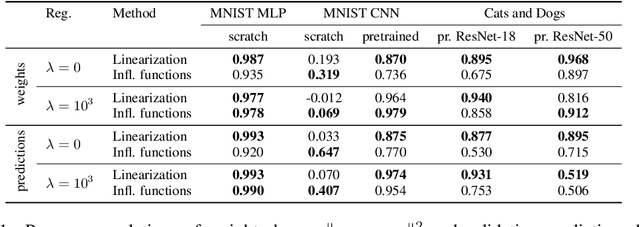

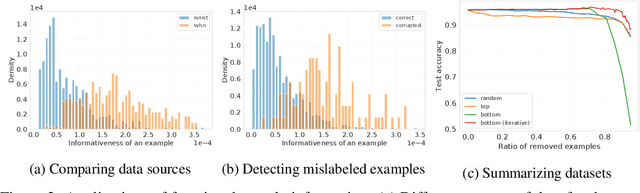
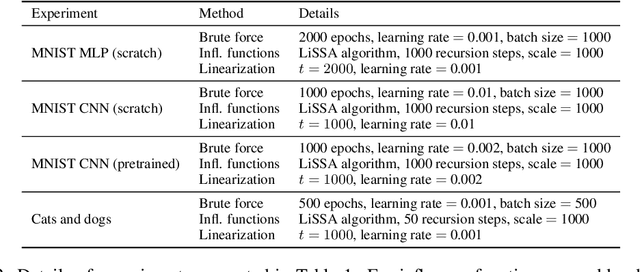
We define a notion of information that an individual sample provides to the training of a neural network, and we specialize it to measure both how much a sample informs the final weights and how much it informs the function computed by the weights. Though related, we show that these quantities have a qualitatively different behavior. We give efficient approximations of these quantities using a linearized network and demonstrate empirically that the approximation is accurate for real-world architectures, such as pre-trained ResNets. We apply these measures to several problems, such as dataset summarization, analysis of under-sampled classes, comparison of informativeness of different data sources, and detection of adversarial and corrupted examples. Our work generalizes existing frameworks but enjoys better computational properties for heavily over-parametrized models, which makes it possible to apply it to real-world networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge