Efficient Gridless DoA Estimation Method of Non-uniform Linear Arrays with Applications in Automotive Radars
Paper and Code
Mar 08, 2023
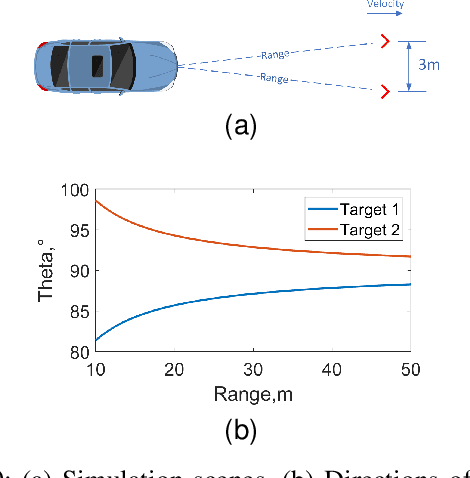
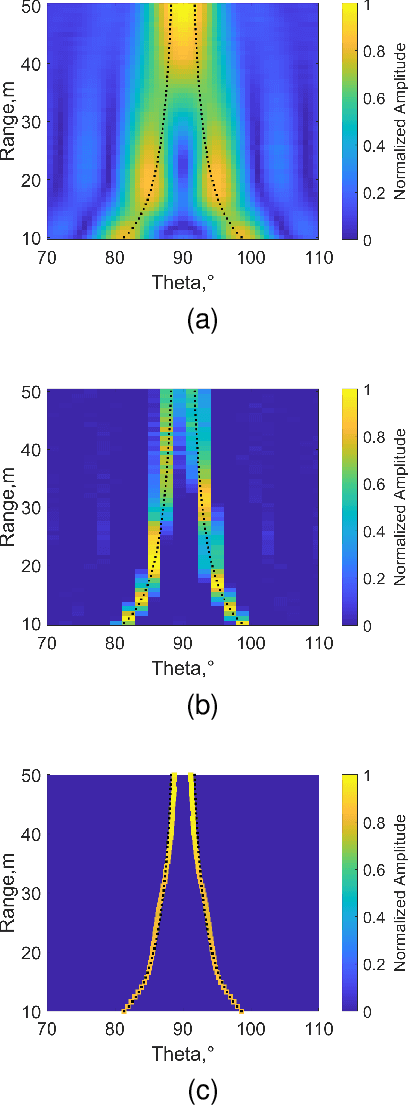

This paper focuses on the gridless direction-of-arrival (DoA) estimation for data acquired by non-uniform linear arrays (NLAs) in automotive applications. Atomic norm minimization (ANM) is a promising gridless sparse recovery algorithm under the Toeplitz model and solved by convex relaxation, thus it is only applicable to uniform linear arrays (ULAs) with array manifolds having a Vandermonde structure. In automotive applications, it is essential to apply the gridless DoA estimation to NLAs with arbitrary geometry with efficiency. In this paper, a fast ANM-based gridless DoA estimation algorithm for NLAs is proposed, which employs the array manifold separation technique and the accelerated proximal gradient (APG) technique, making it applicable to NLAs without losing of efficiency. Simulation and measurement experiments on automotive multiple-input multiple-output (MIMO) radars demonstrate the superiority of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge