Discrete-Valued Neural Communication
Paper and Code
Jul 10, 2021

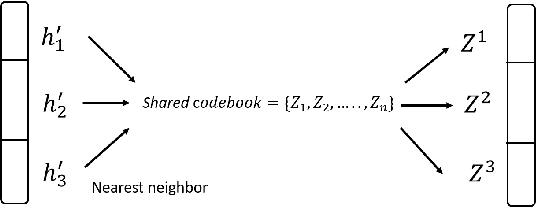
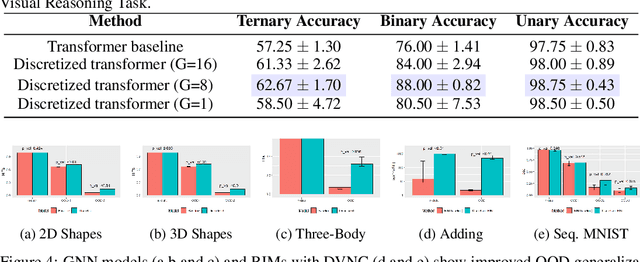
Deep learning has advanced from fully connected architectures to structured models organized into components, e.g., the transformer composed of positional elements, modular architectures divided into slots, and graph neural nets made up of nodes. In structured models, an interesting question is how to conduct dynamic and possibly sparse communication among the separate components. Here, we explore the hypothesis that restricting the transmitted information among components to discrete representations is a beneficial bottleneck. The motivating intuition is human language in which communication occurs through discrete symbols. Even though individuals have different understandings of what a "cat" is based on their specific experiences, the shared discrete token makes it possible for communication among individuals to be unimpeded by individual differences in internal representation. To discretize the values of concepts dynamically communicated among specialist components, we extend the quantization mechanism from the Vector-Quantized Variational Autoencoder to multi-headed discretization with shared codebooks and use it for discrete-valued neural communication (DVNC). Our experiments show that DVNC substantially improves systematic generalization in a variety of architectures -- transformers, modular architectures, and graph neural networks. We also show that the DVNC is robust to the choice of hyperparameters, making the method very useful in practice. Moreover, we establish a theoretical justification of our discretization process, proving that it has the ability to increase noise robustness and reduce the underlying dimensionality of the model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge