Difference in Euclidean Norm Can Cause Semantic Divergence in Batch Normalization

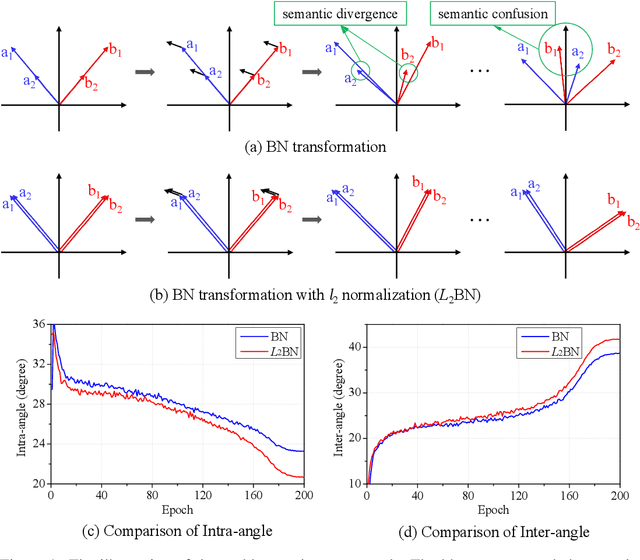
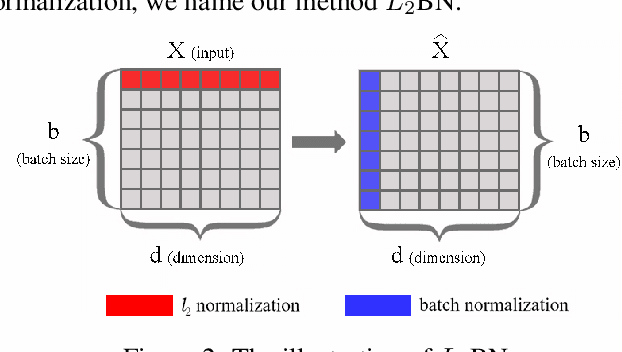
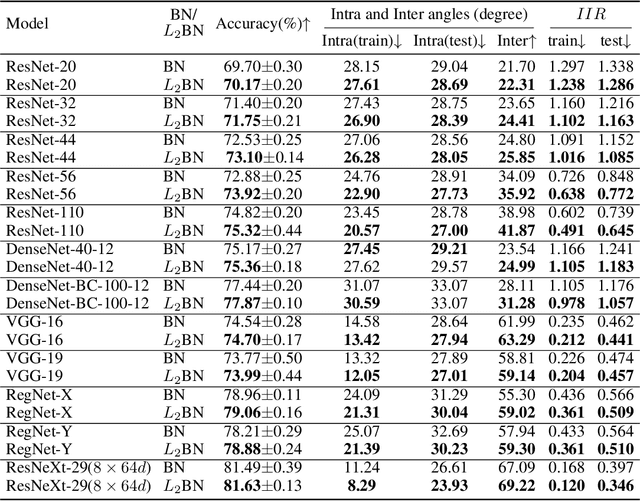
In this paper, we show that the difference in Euclidean norm of samples can make a contribution to the semantic divergence and even confusion, after the spatial translation and scaling transformation in batch normalization. To address this issue, we propose an intuitive but effective method to equalize the Euclidean norms of sample vectors. Concretely, we $l_2$-normalize each sample vector before batch normalization, and therefore the sample vectors are of the same magnitude. Since the proposed method combines the $l_2$ normalization and batch normalization, we name our method as $L_2$BN. The $L_2$BN can strengthen the compactness of intra-class features and enlarge the discrepancy of inter-class features. In addition, it can help the gradient converge to a stable scale. The $L_2$BN is easy to implement and can exert its effect without any additional parameters and hyper-parameters. Therefore, it can be used as a basic normalization method for neural networks. We evaluate the effectiveness of $L_2$BN through extensive experiments with various models on image classification and acoustic scene classification tasks. The experimental results demonstrate that the $L_2$BN is able to boost the generalization ability of various neural network models and achieve considerable performance improvements.