Deep Active Graph Representation Learning
Paper and Code
Oct 30, 2020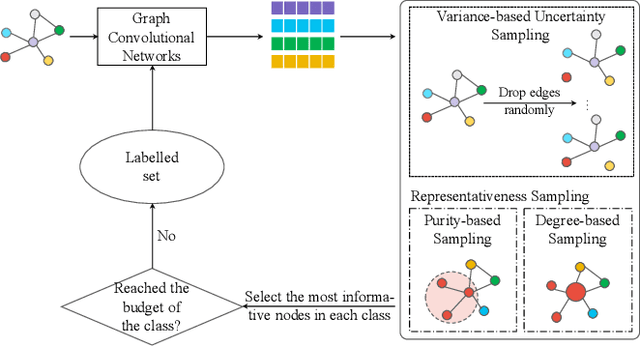
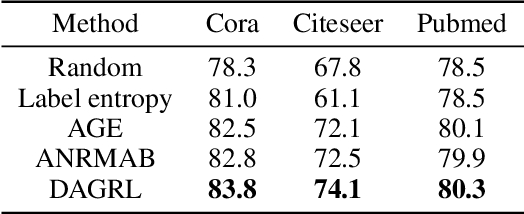
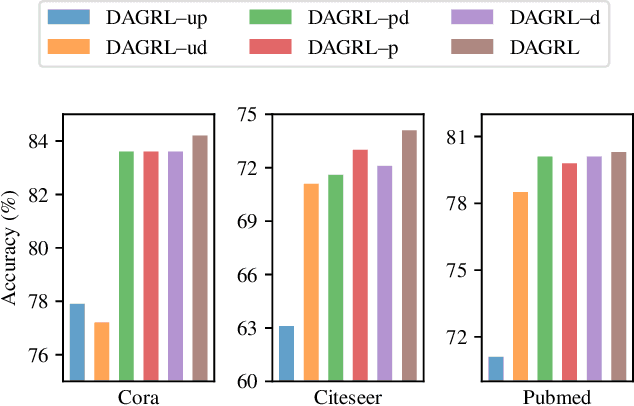
Graph neural networks (GNNs) aim to learn graph representations that preserve both attributive and structural information. In this paper, we study the problem of how to select high-quality nodes for training GNNs, considering GNNs are sensitive to different training datasets. Active learning (AL), whose purpose is to find the most informative instances to maximize the performance of the model, is a promising approach to solve this problem. Previous attempts have combined AL with graph representation learning by designing several selection criteria to measure how informative a node is. However, these methods do not directly utilize both the rich semantic and structural information and are prone to select sparsely-connected nodes (i.e. nodes having few neighbors) and low-purity nodes (i.e. nodes having noisy inter-class edges), which are less effective for training GNN models. To address these problems, we present a Deep Active Graph Representation Learning framework (DAGRL), in which three novel selection criteria are proposed. Specifically, we propose to measure the uncertainty of nodes via random topological perturbation. Besides, we propose two novel representativeness sampling criteria, which utilize both the structural and label information to find densely-connected nodes with many intra-class edges, hence enhance the performance of GNN models significantly. Then, we combine these three criteria with time-sensitive scheduling in accordance to the training progress of GNNs. Furthermore, considering the different size of classes, we employ a novel cluster-aware node selection policy, which ensures the number of selected nodes in each class is proportional to the size of the class. Comprehensive experiments on three public datasets show that our method outperforms previous baselines by a significant margin, which demonstrates its effectiveness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge