Data-Driven Filter Design in FBP: Transforming CT Reconstruction with Trainable Fourier Series
Paper and Code
Jan 29, 2024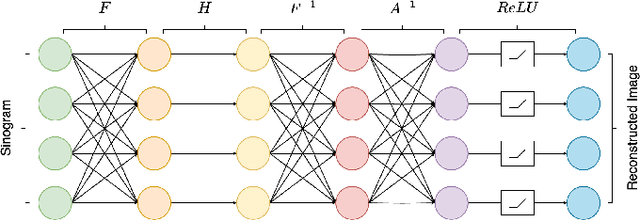
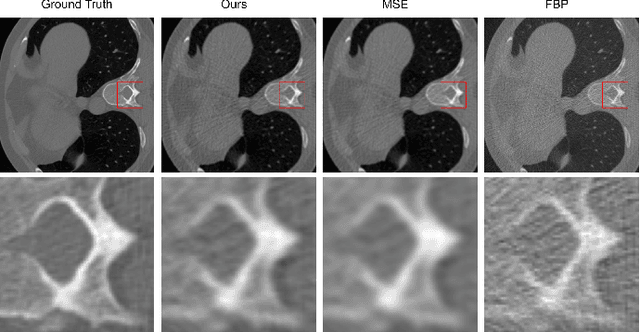
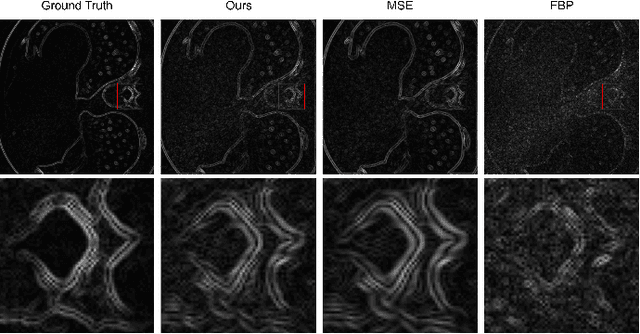
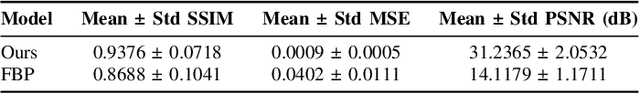
In this study, we introduce a Fourier series-based trainable filter for computed tomography (CT) reconstruction within the filtered backprojection (FBP) framework. This method overcomes the limitation in noise reduction, inherent in conventional FBP methods, by optimizing Fourier series coefficients to construct the filter. This method enables robust performance across different resolution scales and maintains computational efficiency with minimal increment for the trainable parameters compared to other deep learning frameworks. Additionally, we propose Gaussian edge-enhanced (GEE) loss function that prioritizes the $L_1$ norm of high-frequency magnitudes, effectively countering the blurring problems prevalent in mean squared error (MSE) approaches. The model's foundation in the FBP algorithm ensures excellent interpretability, as it relies on a data-driven filter with all other parameters derived through rigorous mathematical procedures. Designed as a plug-and-play solution, our Fourier series-based filter can be easily integrated into existing CT reconstruction models, making it a versatile tool for a wide range of practical applications. Our research presents a robust and scalable method that expands the utility of FBP in both medical and scientific imaging.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge