Contour Moments Based Manipulation of Composite Rigid-Deformable Objects with Finite Time Model Estimation and Shape/Position Control
Paper and Code
Jun 04, 2021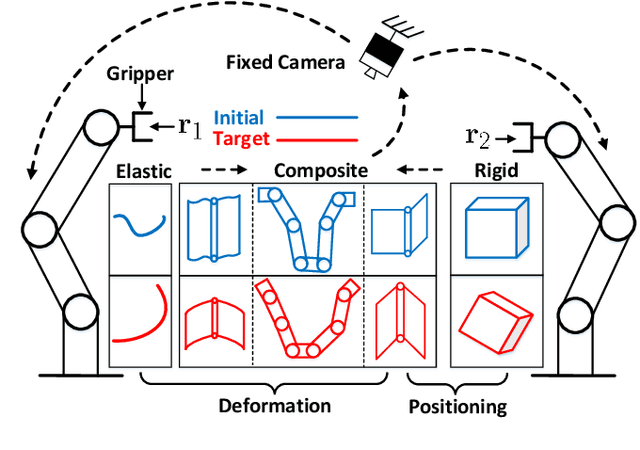
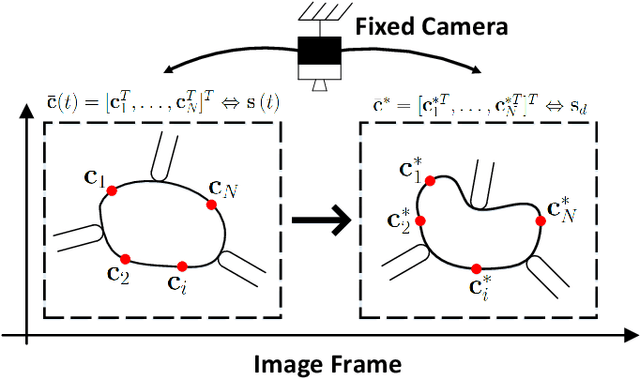
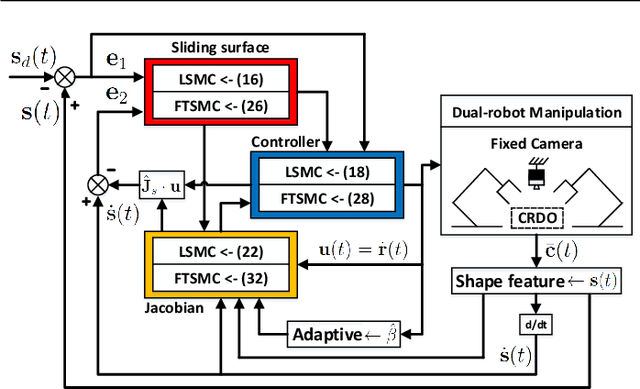
The robotic manipulation of composite rigid-deformable objects (i.e. those with mixed non-homogeneous stiffness properties) is a challenging problem with clear practical applications that, despite the recent progress in the field, it has not been sufficiently studied in the literature. To deal with this issue, in this paper we propose a new visual servoing method that has the capability to manipulate this broad class of objects (which varies from soft to rigid) with the same adaptive strategy. To quantify the object's infinite-dimensional configuration, our new approach computes a compact feedback vector of 2D contour moments features. A sliding mode control scheme is then designed to simultaneously ensure the finite-time convergence of both the feedback shape error and the model estimation error. The stability of the proposed framework (including the boundedness of all the signals) is rigorously proved with Lyapunov theory. Detailed simulations and experiments are presented to validate the effectiveness of the proposed approach. To the best of the author's knowledge, this is the first time that contour moments along with finite-time control have been used to solve this difficult manipulation problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge