Continuous Temporal Graph Networks for Event-Based Graph Data
Paper and Code
May 31, 2022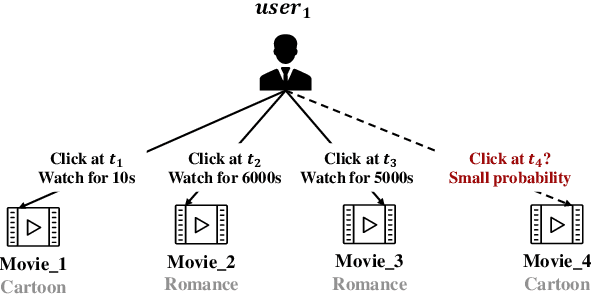
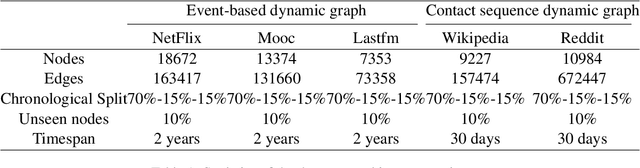
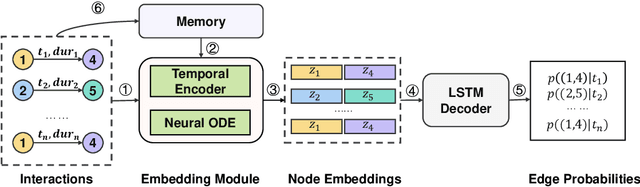
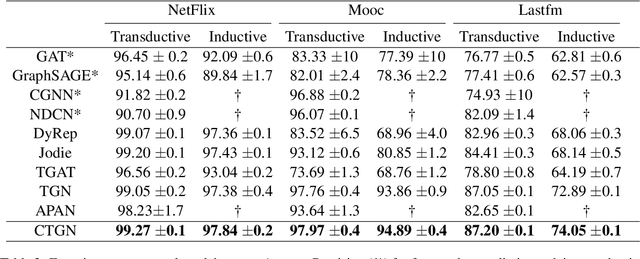
There has been an increasing interest in modeling continuous-time dynamics of temporal graph data. Previous methods encode time-evolving relational information into a low-dimensional representation by specifying discrete layers of neural networks, while real-world dynamic graphs often vary continuously over time. Hence, we propose Continuous Temporal Graph Networks (CTGNs) to capture the continuous dynamics of temporal graph data. We use both the link starting timestamps and link duration as evolving information to model the continuous dynamics of nodes. The key idea is to use neural ordinary differential equations (ODE) to characterize the continuous dynamics of node representations over dynamic graphs. We parameterize ordinary differential equations using a novel graph neural network. The existing dynamic graph networks can be considered as a specific discretization of CTGNs. Experiment results on both transductive and inductive tasks demonstrate the effectiveness of our proposed approach over competitive baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge