ContiFormer: Continuous-Time Transformer for Irregular Time Series Modeling
Paper and Code
Feb 16, 2024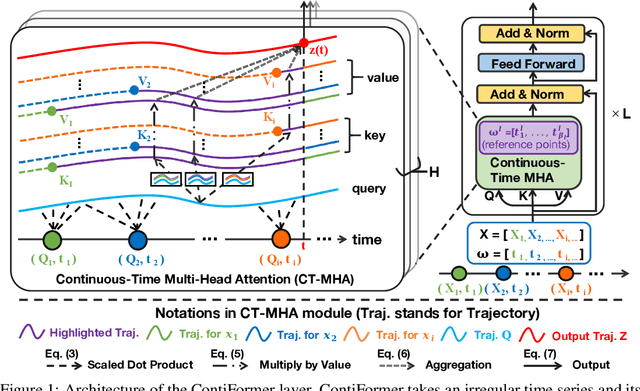
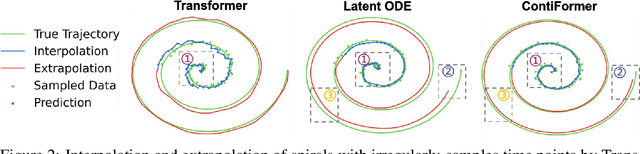
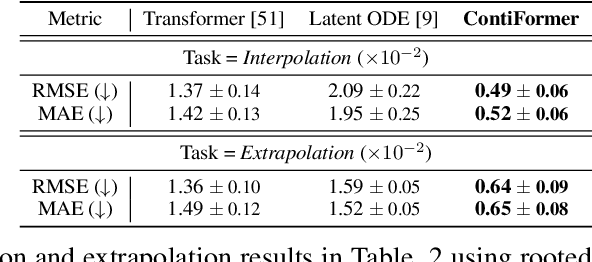
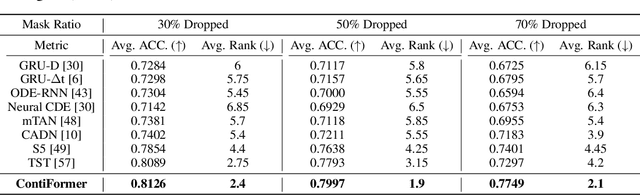
Modeling continuous-time dynamics on irregular time series is critical to account for data evolution and correlations that occur continuously. Traditional methods including recurrent neural networks or Transformer models leverage inductive bias via powerful neural architectures to capture complex patterns. However, due to their discrete characteristic, they have limitations in generalizing to continuous-time data paradigms. Though neural ordinary differential equations (Neural ODEs) and their variants have shown promising results in dealing with irregular time series, they often fail to capture the intricate correlations within these sequences. It is challenging yet demanding to concurrently model the relationship between input data points and capture the dynamic changes of the continuous-time system. To tackle this problem, we propose ContiFormer that extends the relation modeling of vanilla Transformer to the continuous-time domain, which explicitly incorporates the modeling abilities of continuous dynamics of Neural ODEs with the attention mechanism of Transformers. We mathematically characterize the expressive power of ContiFormer and illustrate that, by curated designs of function hypothesis, many Transformer variants specialized in irregular time series modeling can be covered as a special case of ContiFormer. A wide range of experiments on both synthetic and real-world datasets have illustrated the superior modeling capacities and prediction performance of ContiFormer on irregular time series data. The project link is https://seqml.github.io/contiformer/.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge