Conditional Sum-Product Networks: Imposing Structure on Deep Probabilistic Architectures
Paper and Code
May 21, 2019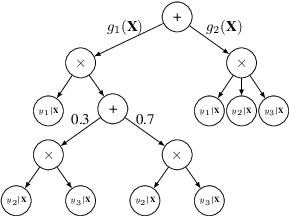
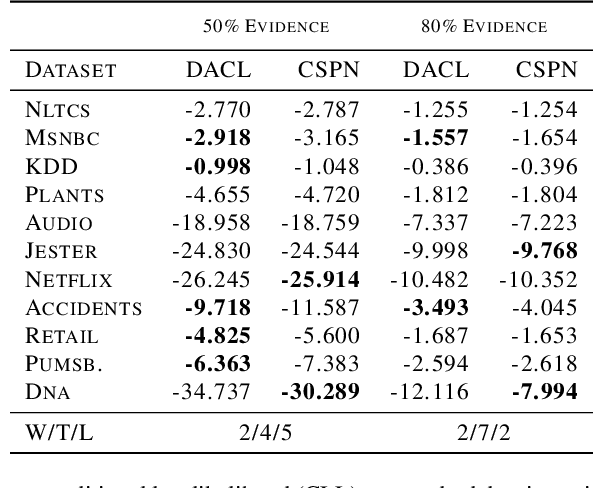
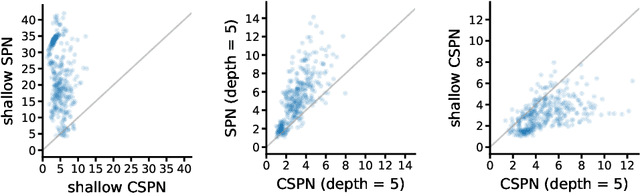

Bayesian networks are a central tool in machine learning and artificial intelligence, and make use of conditional independencies to impose structure on joint distributions. However, they are generally not as expressive as deep learning models and inference is hard and slow. In contrast, deep probabilistic models such as sum-product networks (SPNs) capture joint distributions in a tractable fashion, but use little interpretable structure. Here, we extend the notion of SPNs towards conditional distributions, which combine simple conditional models into high-dimensional ones. As shown in our experiments, the resulting conditional SPNs can be naturally used to impose structure on deep probabilistic models, allow for mixed data types, while maintaining fast and efficient inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge