Bidirectional Loss Function for Label Enhancement and Distribution Learning
Paper and Code
Jul 07, 2020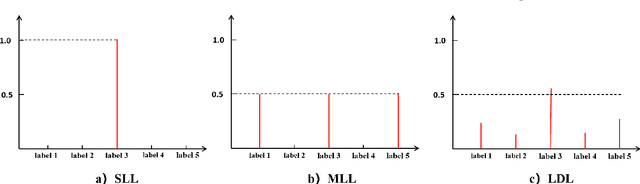

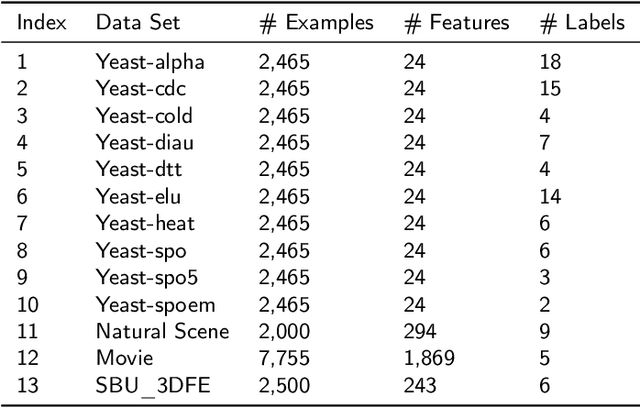
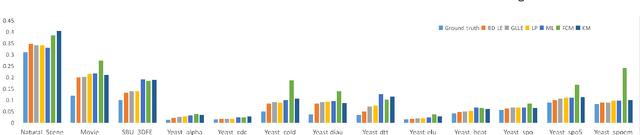
Label distribution learning (LDL) is an interpretable and general learning paradigm that has been applied in many real-world applications. In contrast to the simple logical vector in single-label learning (SLL) and multi-label learning (MLL), LDL assigns labels with a description degree to each instance. In practice, two challenges exist in LDL, namely, how to address the dimensional gap problem during the learning process of LDL and how to exactly recover label distributions from existing logical labels, i.e., Label Enhancement (LE). For most existing LDL and LE algorithms, the fact that the dimension of the input matrix is much higher than that of the output one is alway ignored and it typically leads to the dimensional reduction owing to the unidirectional projection. The valuable information hidden in the feature space is lost during the mapping process. To this end, this study considers bidirectional projections function which can be applied in LE and LDL problems simultaneously. More specifically, this novel loss function not only considers the mapping errors generated from the projection of the input space into the output one but also accounts for the reconstruction errors generated from the projection of the output space back to the input one. This loss function aims to potentially reconstruct the input data from the output data. Therefore, it is expected to obtain more accurate results. Finally, experiments on several real-world datasets are carried out to demonstrate the superiority of the proposed method for both LE and LDL.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge