BALSON: Bayesian Least Squares Optimization with Nonnegative L1-Norm Constraint
Paper and Code
Jul 08, 2018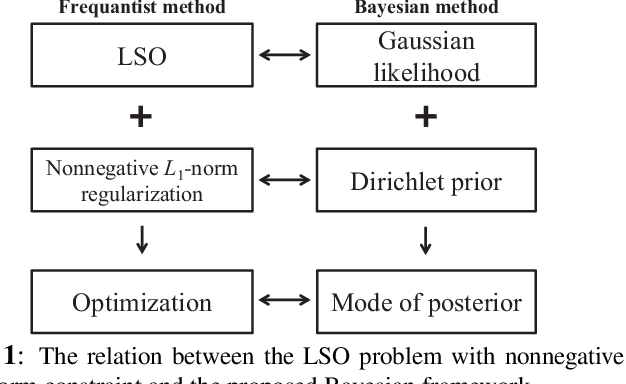
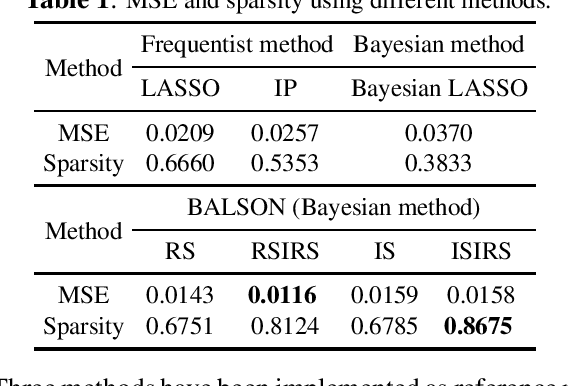
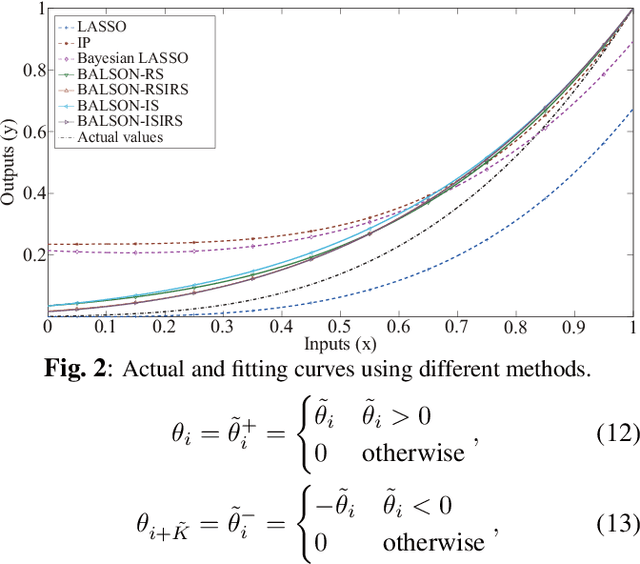
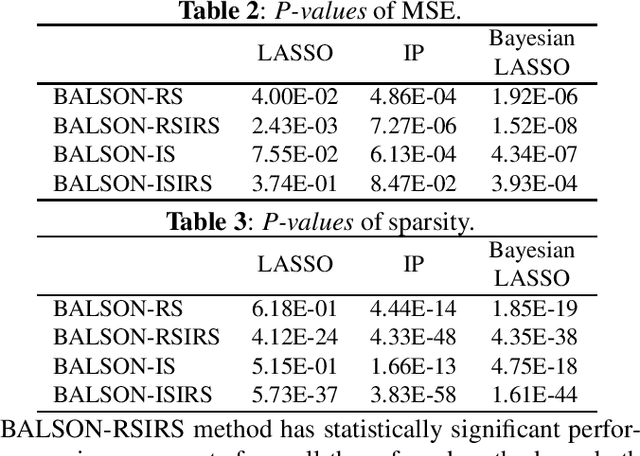
A Bayesian approach termed BAyesian Least Squares Optimization with Nonnegative L1-norm constraint (BALSON) is proposed. The error distribution of data fitting is described by Gaussian likelihood. The parameter distribution is assumed to be a Dirichlet distribution. With the Bayes rule, searching for the optimal parameters is equivalent to finding the mode of the posterior distribution. In order to explicitly characterize the nonnegative L1-norm constraint of the parameters, we further approximate the true posterior distribution by a Dirichlet distribution. We estimate the statistics of the approximating Dirichlet posterior distribution by sampling methods. Four sampling methods have been introduced. With the estimated posterior distributions, the original parameters can be effectively reconstructed in polynomial fitting problems, and the BALSON framework is found to perform better than conventional methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge