ASVRG: Accelerated Proximal SVRG
Paper and Code
Oct 07, 2018
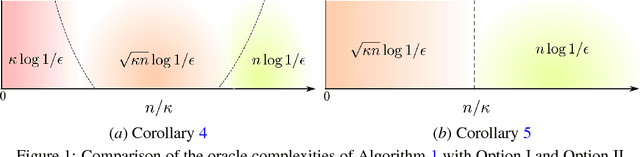
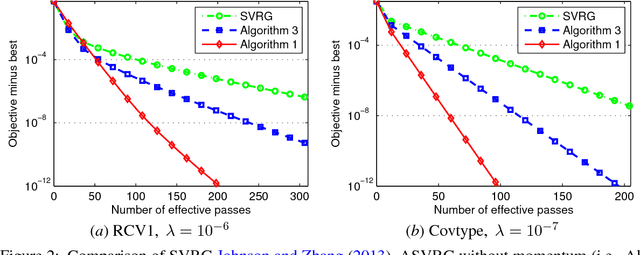
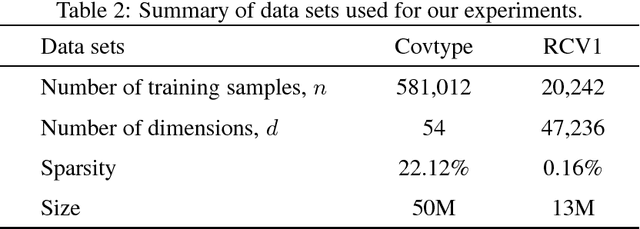
This paper proposes an accelerated proximal stochastic variance reduced gradient (ASVRG) method, in which we design a simple and effective momentum acceleration trick. Unlike most existing accelerated stochastic variance reduction methods such as Katyusha, ASVRG has only one additional variable and one momentum parameter. Thus, ASVRG is much simpler than those methods, and has much lower per-iteration complexity. We prove that ASVRG achieves the best known oracle complexities for both strongly convex and non-strongly convex objectives. In addition, we extend ASVRG to mini-batch and non-smooth settings. We also empirically verify our theoretical results and show that the performance of ASVRG is comparable with, and sometimes even better than that of the state-of-the-art stochastic methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge