Analyzing and Mitigating Interference in Neural Architecture Search

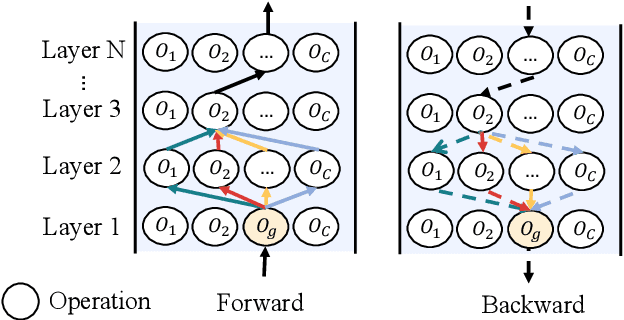
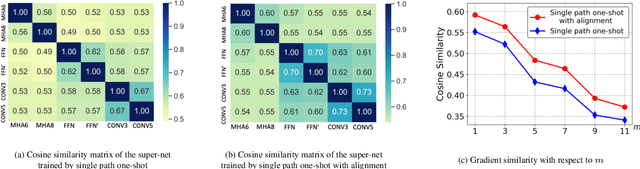
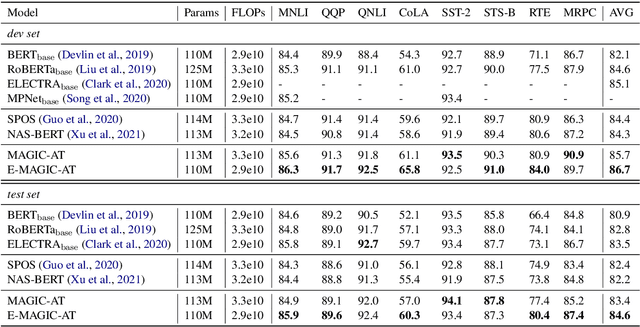
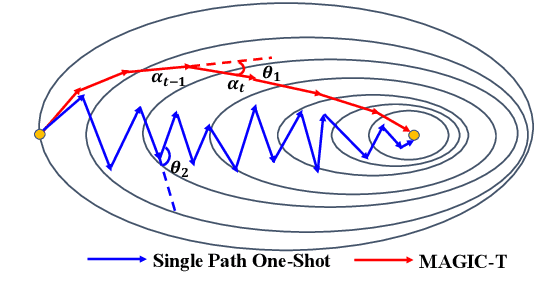
Weight sharing has become the \textit{de facto} approach to reduce the training cost of neural architecture search (NAS) by reusing the weights of shared operators from previously trained child models. However, the estimated accuracy of those child models has a low rank correlation with the ground truth accuracy due to the interference among different child models caused by weight sharing. In this paper, we investigate the interference issue by sampling different child models and calculating the gradient similarity of shared operators, and observe that: 1) the interference on a shared operator between two child models is positively correlated to the number of different operators between them; 2) the interference is smaller when the inputs and outputs of the shared operator are more similar. Inspired by these two observations, we propose two approaches to mitigate the interference: 1) rather than randomly sampling child models for optimization, we propose a gradual modification scheme by modifying one operator between adjacent optimization steps to minimize the interference on the shared operators; 2) forcing the inputs and outputs of the operator across all child models to be similar to reduce the interference. Experiments on a BERT search space verify that mitigating interference via each of our proposed methods improves the rank correlation of super-pet and combining both methods can achieve better results. Our searched architecture outperforms RoBERTa$_{\rm base}$ by 1.1 and 0.6 scores and ELECTRA$_{\rm base}$ by 1.6 and 1.1 scores on the dev and test set of GLUE benchmark. Extensive results on the BERT compression task, SQuAD datasets and other search spaces also demonstrate the effectiveness and generality of our proposed methods.