Adaptive Federated Learning Over the Air
Paper and Code
Mar 11, 2024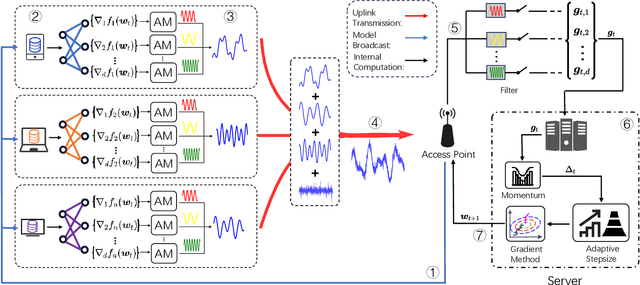
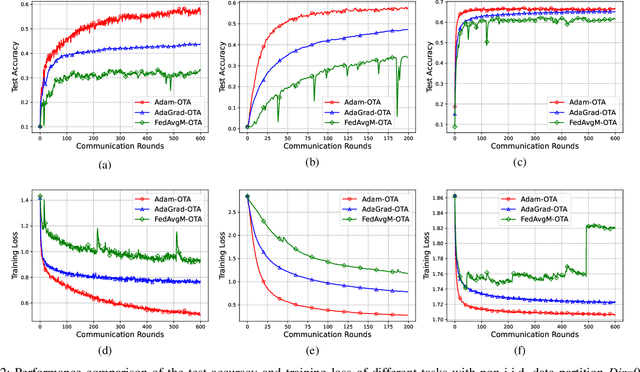
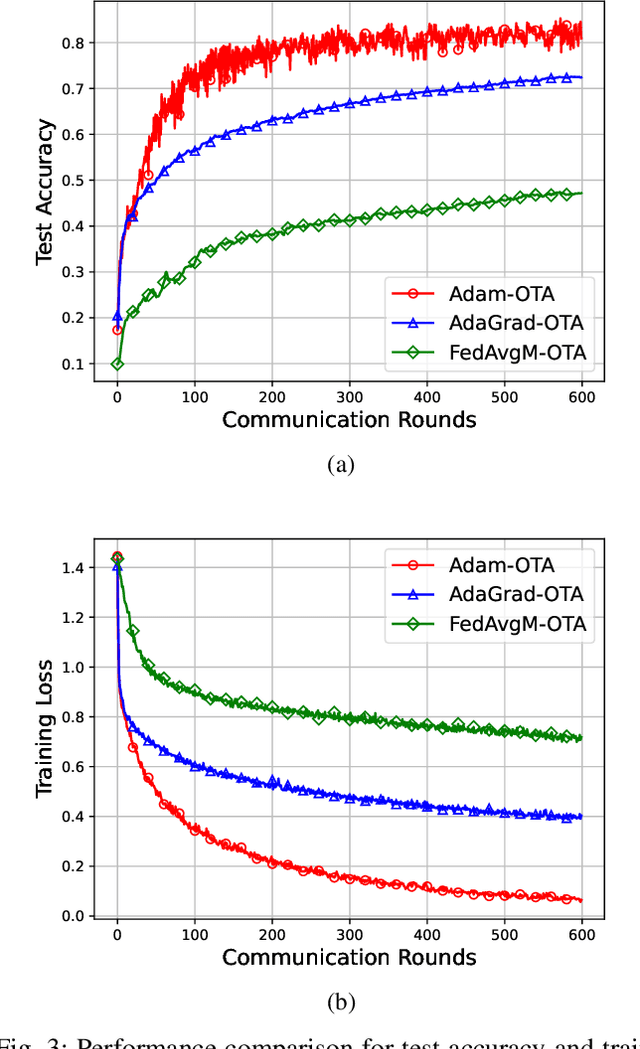
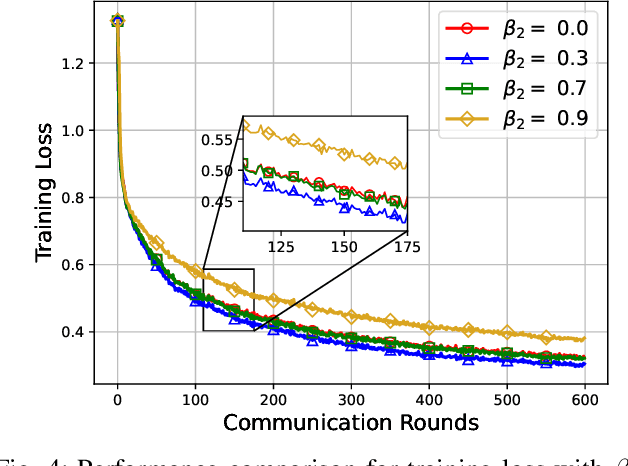
We propose a federated version of adaptive gradient methods, particularly AdaGrad and Adam, within the framework of over-the-air model training. This approach capitalizes on the inherent superposition property of wireless channels, facilitating fast and scalable parameter aggregation. Meanwhile, it enhances the robustness of the model training process by dynamically adjusting the stepsize in accordance with the global gradient update. We derive the convergence rate of the training algorithms, encompassing the effects of channel fading and interference, for a broad spectrum of nonconvex loss functions. Our analysis shows that the AdaGrad-based algorithm converges to a stationary point at the rate of $\mathcal{O}( \ln{(T)} /{ T^{ 1 - \frac{1}{\alpha} } } )$, where $\alpha$ represents the tail index of the electromagnetic interference. This result indicates that the level of heavy-tailedness in interference distribution plays a crucial role in the training efficiency: the heavier the tail, the slower the algorithm converges. In contrast, an Adam-like algorithm converges at the $\mathcal{O}( 1/T )$ rate, demonstrating its advantage in expediting the model training process. We conduct extensive experiments that corroborate our theoretical findings and affirm the practical efficacy of our proposed federated adaptive gradient methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge