Accelerated Experimental Design for Pairwise Comparisons
Paper and Code
Jan 18, 2019

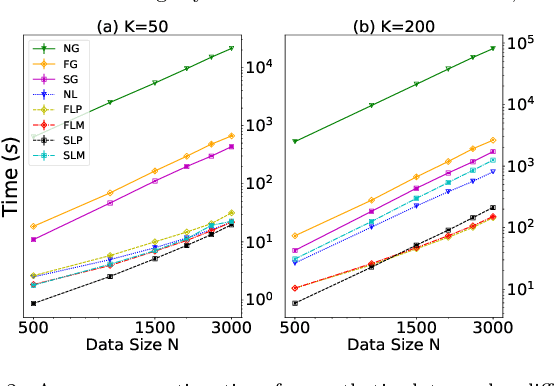
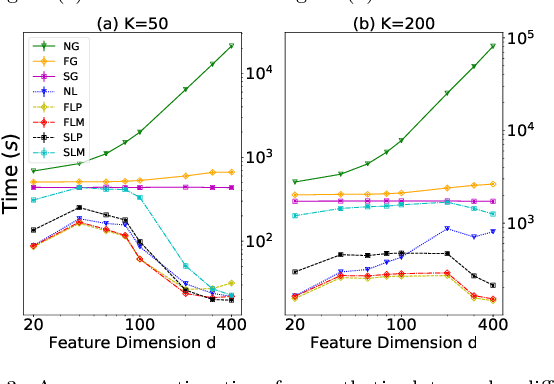
Pairwise comparison labels are more informative and less variable than class labels, but generating them poses a challenge: their number grows quadratically in the dataset size. We study a natural experimental design objective, namely, D-optimality, that can be used to identify which $K$ pairwise comparisons to generate. This objective is known to perform well in practice, and is submodular, making the selection approximable via the greedy algorithm. A na\"ive greedy implementation has $O(N^2d^2K)$ complexity, where $N$ is the dataset size, $d$ is the feature space dimension, and $K$ is the number of generated comparisons. We show that, by exploiting the inherent geometry of the dataset--namely, that it consists of pairwise comparisons--the greedy algorithm's complexity can be reduced to $O(N^2(K+d)+N(dK+d^2) +d^2K).$ We apply the same acceleration also to the so-called lazy greedy algorithm. When combined, the above improvements lead to an execution time of less than 1 hour for a dataset with $10^8$ comparisons; the na\"ive greedy algorithm on the same dataset would require more than 10 days to terminate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge