A Game-Theoretic Approach for Improving Generalization Ability of TSP Solvers
Paper and Code
Oct 29, 2021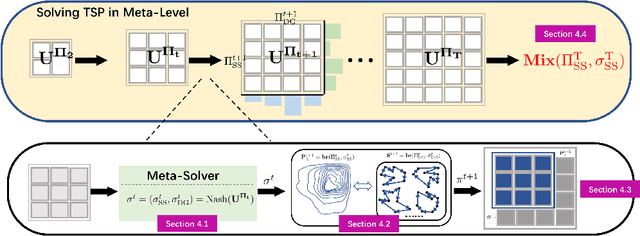
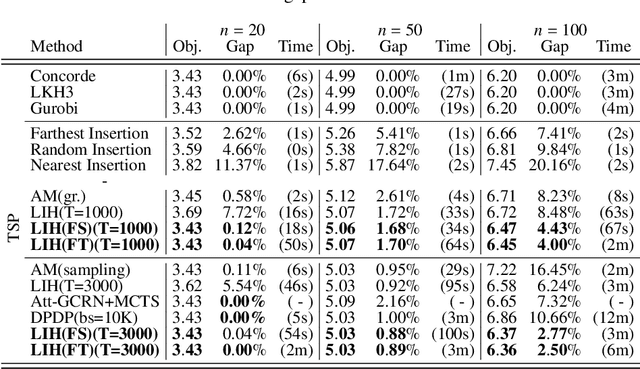
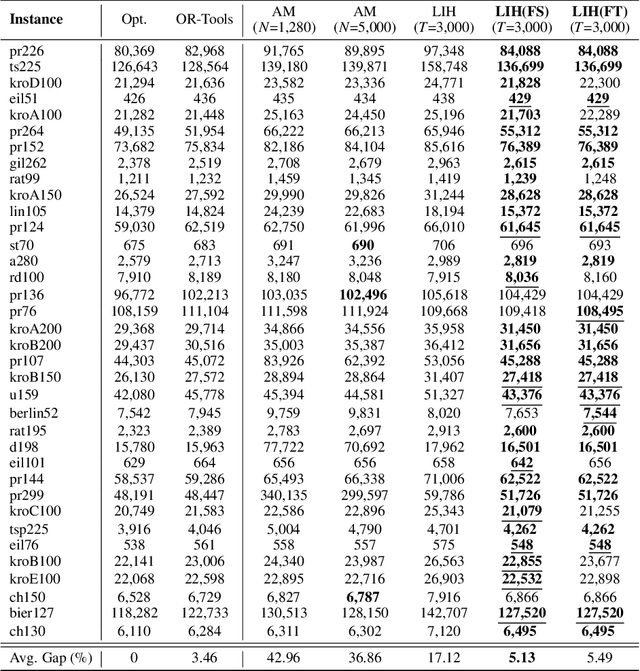
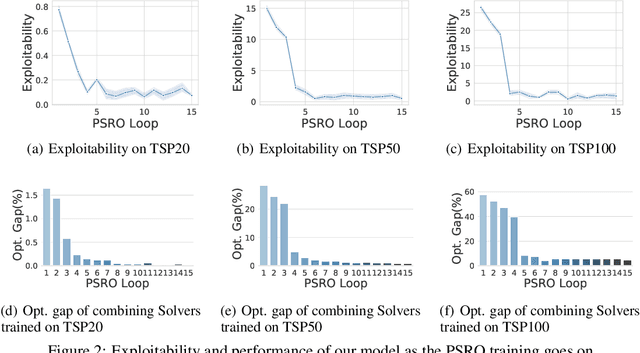
In this paper, we shed new light on the generalization ability of deep learning-based solvers for Traveling Salesman Problems (TSP). Specifically, we introduce a two-player zero-sum framework between a trainable \emph{Solver} and a \emph{Data Generator}, where the Solver aims to solve the task instances provided by the Generator, and the Generator aims to generate increasingly difficult instances for improving the Solver. Grounded in \textsl{Policy Space Response Oracle} (PSRO) methods, our two-player framework outputs a population of best-responding Solvers, over which we can mix and output a combined model that achieves the least exploitability against the Generator, and thereby the most generalizable performance on different TSP tasks. We conduct experiments on a variety of TSP instances with different types and sizes. Results suggest that our Solvers achieve the state-of-the-art performance even on tasks the Solver never meets, whilst the performance of other deep learning-based Solvers drops sharply due to over-fitting. On real-world instances from \textsc{TSPLib}, our method also attains a \textbf{12\%} improvement, in terms of optimal gap, over the best baseline model. To demonstrate the principle of our framework, we study the learning outcome of the proposed two-player game and demonstrate that the exploitability of the Solver population decreases during training, and it eventually approximates the Nash equilibrium along with the Generator.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge