an Zhang
Uncertainty Quantification via Hölder Divergence for Multi-View Representation Learning
Oct 29, 2024
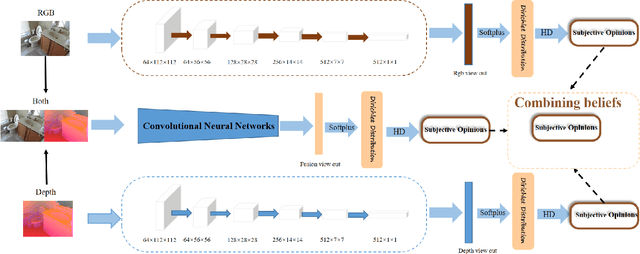
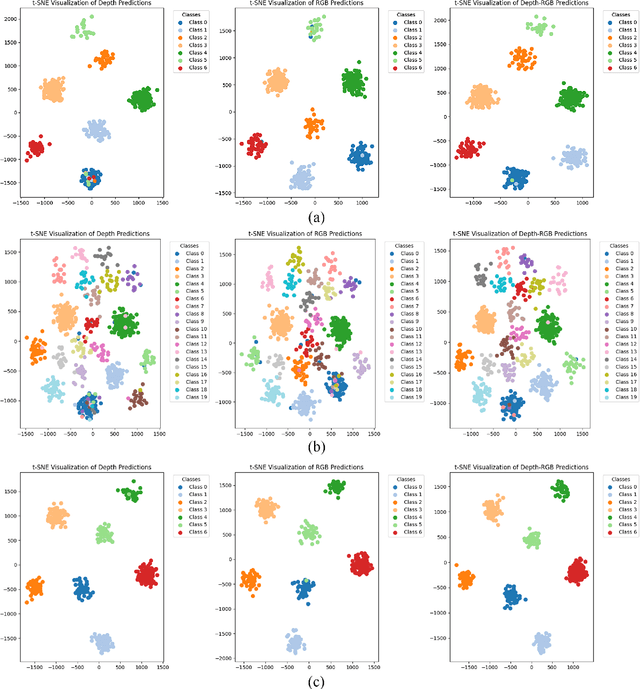

Abstract:Evidence-based deep learning represents a burgeoning paradigm for uncertainty estimation, offering reliable predictions with negligible extra computational overheads. Existing methods usually adopt Kullback-Leibler divergence to estimate the uncertainty of network predictions, ignoring domain gaps among various modalities. To tackle this issue, this paper introduces a novel algorithm based on H\"older Divergence (HD) to enhance the reliability of multi-view learning by addressing inherent uncertainty challenges from incomplete or noisy data. Generally, our method extracts the representations of multiple modalities through parallel network branches, and then employs HD to estimate the prediction uncertainties. Through the Dempster-Shafer theory, integration of uncertainty from different modalities, thereby generating a comprehensive result that considers all available representations. Mathematically, HD proves to better measure the ``distance'' between real data distribution and predictive distribution of the model and improve the performances of multi-class recognition tasks. Specifically, our method surpass the existing state-of-the-art counterparts on all evaluating benchmarks. We further conduct extensive experiments on different backbones to verify our superior robustness. It is demonstrated that our method successfully pushes the corresponding performance boundaries. Finally, we perform experiments on more challenging scenarios, \textit{i.e.}, learning with incomplete or noisy data, revealing that our method exhibits a high tolerance to such corrupted data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge