A General Framework for Data-Use Auditing of ML Models

Auditing the use of data in training machine-learning (ML) models is an increasingly pressing challenge, as myriad ML practitioners routinely leverage the effort of content creators to train models without their permission. In this paper, we propose a general method to audit an ML model for the use of a data-owner's data in training, without prior knowledge of the ML task for which the data might be used. Our method leverages any existing black-box membership inference method, together with a sequential hypothesis test of our own design, to detect data use with a quantifiable, tunable false-detection rate. We show the effectiveness of our proposed framework by applying it to audit data use in two types of ML models, namely image classifiers and foundation models.

Mendata: A Framework to Purify Manipulated Training Data

Untrusted data used to train a model might have been manipulated to endow the learned model with hidden properties that the data contributor might later exploit. Data purification aims to remove such manipulations prior to training the model. We propose Mendata, a novel framework to purify manipulated training data. Starting from a small reference dataset in which a large majority of the inputs are clean, Mendata perturbs the training inputs so that they retain their utility but are distributed similarly (as measured by Wasserstein distance) to the reference data, thereby eliminating hidden properties from the learned model. A key challenge is how to find such perturbations, which we address by formulating a min-max optimization problem and developing a two-step method to iteratively solve it. We demonstrate the effectiveness of Mendata by applying it to defeat state-of-the-art data poisoning and data tracing techniques.

Differentially Private ADMM for Convex Distributed Learning: Improved Accuracy via Multi-Step Approximation

Alternating Direction Method of Multipliers (ADMM) is a popular algorithm for distributed learning, where a network of nodes collaboratively solve a regularized empirical risk minimization by iterative local computation associated with distributed data and iterate exchanges. When the training data is sensitive, the exchanged iterates will cause serious privacy concern. In this paper, we aim to propose a new differentially private distributed ADMM algorithm with improved accuracy for a wide range of convex learning problems. In our proposed algorithm, we adopt the approximation of the objective function in the local computation to introduce calibrated noise into iterate updates robustly, and allow multiple primal variable updates per node in each iteration. Our theoretical results demonstrate that our approach can obtain higher utility by such multiple approximate updates, and achieve the error bounds asymptotic to the state-of-art ones for differentially private empirical risk minimization.

DP-ADMM: ADMM-based Distributed Learning with Differential Privacy

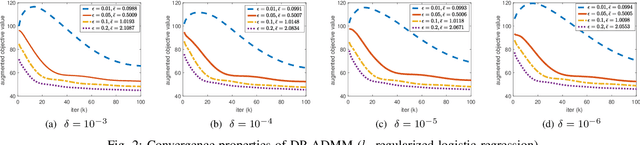
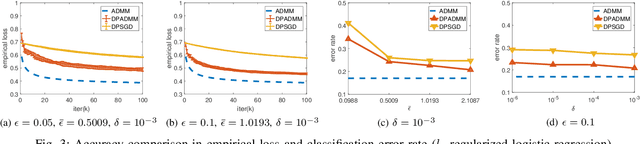
Privacy-preserving distributed machine learning has become more important than ever due to the high demand of large-scale data processing. This paper focuses on a class of machine learning problems that can be formulated as regularized empirical risk minimization, and develops a privacy-preserving approach to such learning problems. We use Alternating Direction Method of Multipliers (ADMM) to decentralize the learning algorithm, and apply Gaussian mechanisms to provide local differential privacy guarantee. However, simply combining ADMM and local randomization mechanisms would result in a nonconvergent algorithm with bad performance even under moderate privacy guarantees. Besides, this approach cannot be applied when the objective functions of the learning problems are non-smooth. To address these concerns, we propose an improved ADMM-based Differentially Private distributed learning algorithm, DP-ADMM, where an approximate augmented Lagrangian function and Gaussian mechanisms with time-varying variance are utilized. We also apply the moment accountant method to bound the total privacy loss. Our theoretical analysis shows that DP-ADMM can be applied to convex learning problems with both smooth and non-smooth objectives, provides differential privacy guarantee, and achieves a convergence rate of $O(1/\sqrt{t})$, where $t$ is the number of iterations. Our evaluations demonstrate that our approach can achieve good convergence and accuracy with strong privacy guarantee.