DP-ADMM: ADMM-based Distributed Learning with Differential Privacy
Paper and Code
Sep 03, 2018
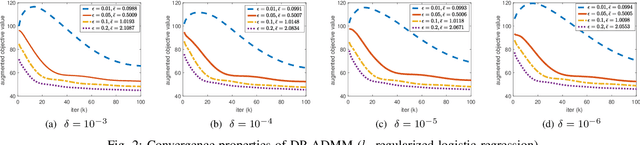
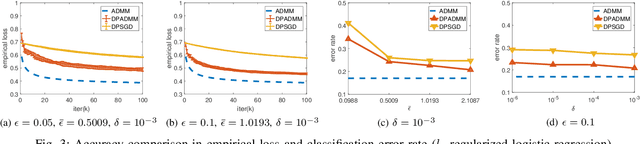

Privacy-preserving distributed machine learning has become more important than ever due to the high demand of large-scale data processing. This paper focuses on a class of machine learning problems that can be formulated as regularized empirical risk minimization, and develops a privacy-preserving approach to such learning problems. We use Alternating Direction Method of Multipliers (ADMM) to decentralize the learning algorithm, and apply Gaussian mechanisms to provide local differential privacy guarantee. However, simply combining ADMM and local randomization mechanisms would result in a nonconvergent algorithm with bad performance even under moderate privacy guarantees. Besides, this approach cannot be applied when the objective functions of the learning problems are non-smooth. To address these concerns, we propose an improved ADMM-based Differentially Private distributed learning algorithm, DP-ADMM, where an approximate augmented Lagrangian function and Gaussian mechanisms with time-varying variance are utilized. We also apply the moment accountant method to bound the total privacy loss. Our theoretical analysis shows that DP-ADMM can be applied to convex learning problems with both smooth and non-smooth objectives, provides differential privacy guarantee, and achieves a convergence rate of $O(1/\sqrt{t})$, where $t$ is the number of iterations. Our evaluations demonstrate that our approach can achieve good convergence and accuracy with strong privacy guarantee.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge