On LASSO Inference for High Dimensional Predictive Regression

LASSO introduces shrinkage bias into estimated coefficients, which can adversely affect the desirable asymptotic normality and invalidate the standard inferential procedure based on the $t$-statistic. The desparsified LASSO has emerged as a well-known remedy for this issue. In the context of high dimensional predictive regression, the desparsified LASSO faces an additional challenge: the Stambaugh bias arising from nonstationary regressors. To restore the standard inferential procedure, we propose a novel estimator called IVX-desparsified LASSO (XDlasso). XDlasso eliminates the shrinkage bias and the Stambaugh bias simultaneously and does not require prior knowledge about the identities of nonstationary and stationary regressors. We establish the asymptotic properties of XDlasso for hypothesis testing, and our theoretical findings are supported by Monte Carlo simulations. Applying our method to real-world applications from the FRED-MD database -- which includes a rich set of control variables -- we investigate two important empirical questions: (i) the predictability of the U.S. stock returns based on the earnings-price ratio, and (ii) the predictability of the U.S. inflation using the unemployment rate.

On LASSO for High Dimensional Predictive Regression

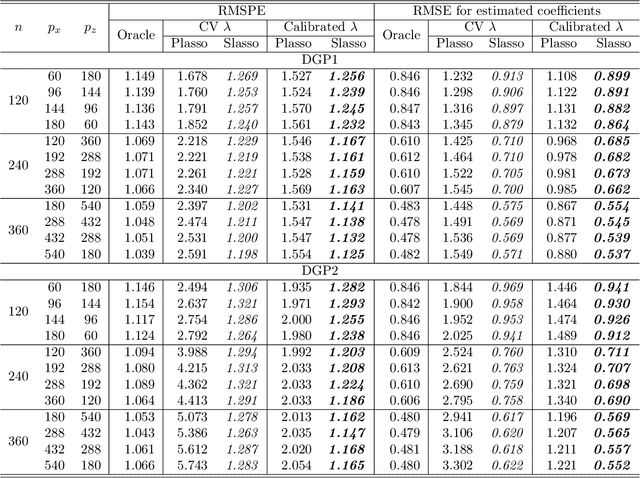
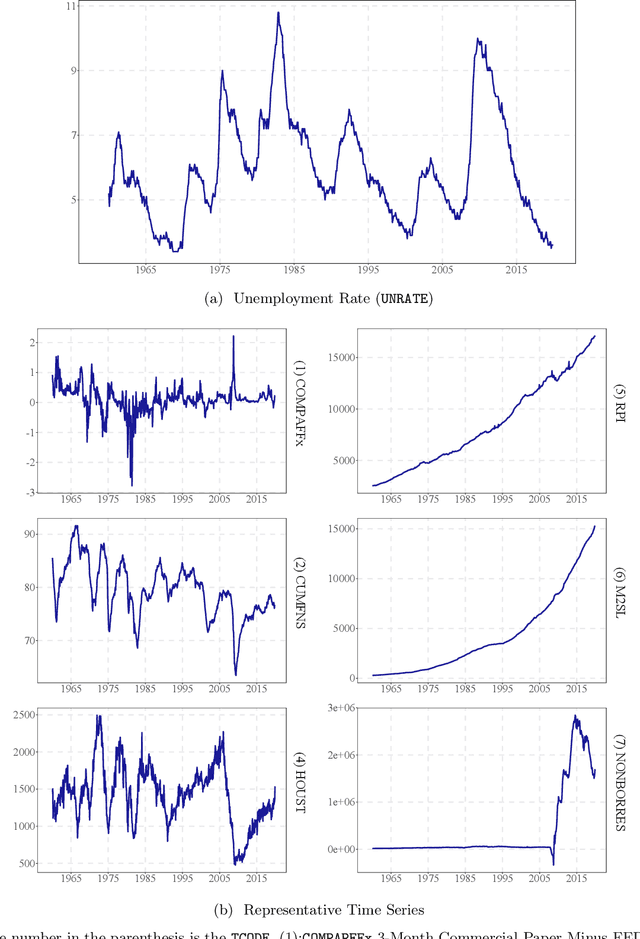
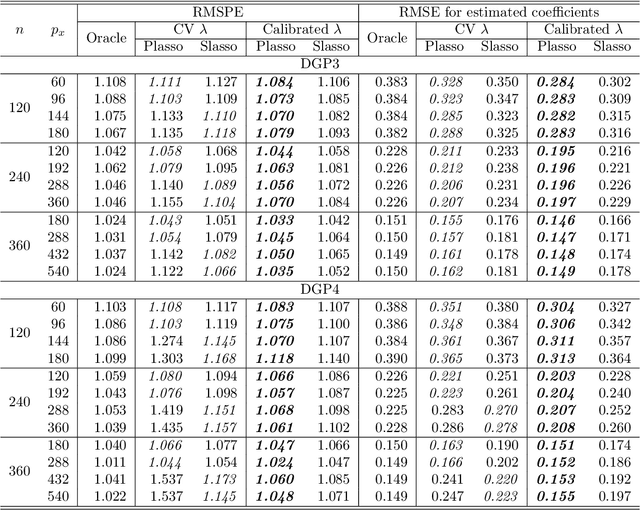
In a high dimensional linear predictive regression where the number of potential predictors can be larger than the sample size, we consider using LASSO, a popular L1-penalized regression method, to estimate the sparse coefficients when many unit root regressors are present. Consistency of LASSO relies on two building blocks: the deviation bound of the cross product of the regressors and the error term, and the restricted eigenvalue of the Gram matrix of the regressors. In our setting where unit root regressors are driven by temporal dependent non-Gaussian innovations, we establish original probabilistic bounds for these two building blocks. The bounds imply that the rates of convergence of LASSO are different from those in the familiar cross sectional case. In practical applications given a mixture of stationary and nonstationary predictors, asymptotic guarantee of LASSO is preserved if all predictors are scale-standardized. In an empirical example of forecasting the unemployment rate with many macroeconomic time series, strong performance is delivered by LASSO when the initial specification is guided by macroeconomic domain expertise.

The boosted HP filter is more general than you might think

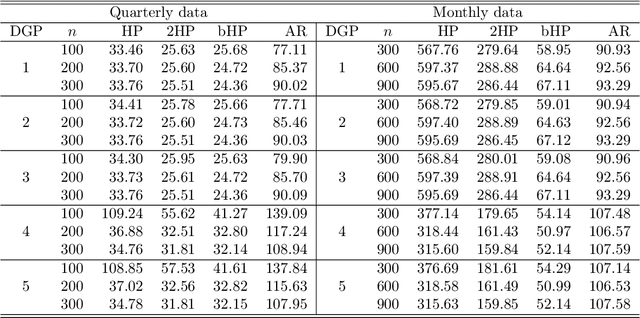
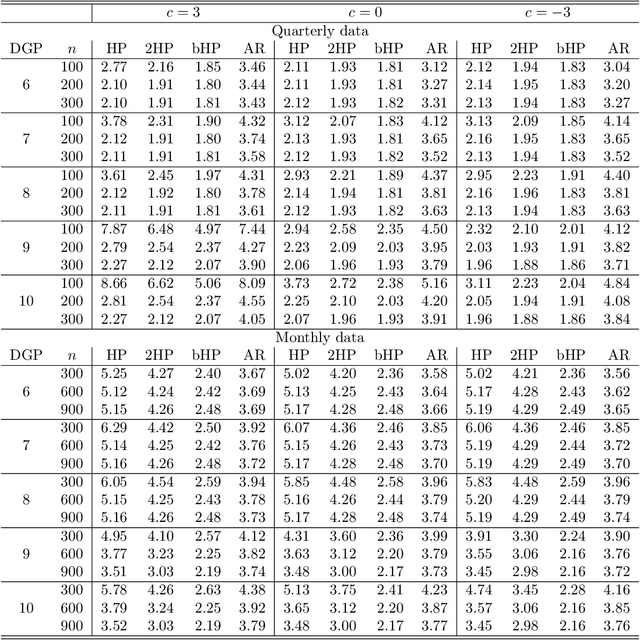
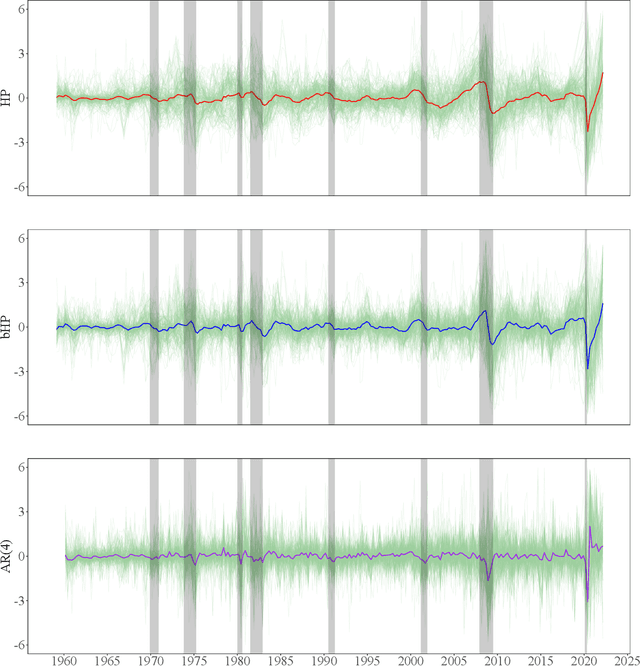
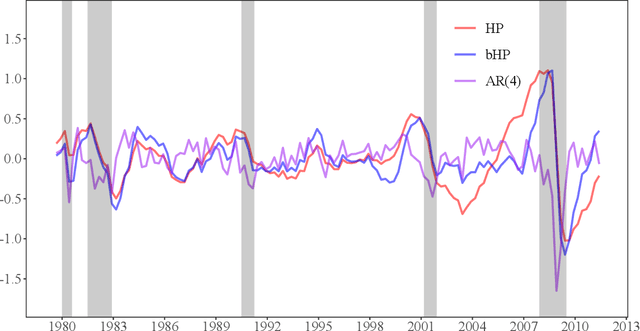
The global financial crisis and Covid recession have renewed discussion concerning trend-cycle discovery in macroeconomic data, and boosting has recently upgraded the popular HP filter to a modern machine learning device suited to data-rich and rapid computational environments. This paper sheds light on its versatility in trend-cycle determination, explaining in a simple manner both HP filter smoothing and the consistency delivered by boosting for general trend detection. Applied to a universe of time series in FRED databases, boosting outperforms other methods in timely capturing downturns at crises and recoveries that follow. With its wide applicability the boosted HP filter is a useful automated machine learning addition to the macroeconometric toolkit.

Testing Overidentifying Restrictions with High-Dimensional Data and Heteroskedasticity

This paper proposes a new test of overidentifying restrictions (called the Q test) with high-dimensional data. This test is based on estimation and inference for a quadratic form of high-dimensional parameters. It is shown to have the desired asymptotic size and power properties under heteroskedasticity, even if the number of instruments and covariates is larger than the sample size. Simulation results show that the new test performs favorably compared to existing alternative tests (Chao et al., 2014; Kolesar, 2018; Carrasco and Doukali, 2021) under the scenarios when those tests are feasible or not. An empirical example of the trade and economic growth nexus manifests the usefulness of the proposed test.