The boosted HP filter is more general than you might think

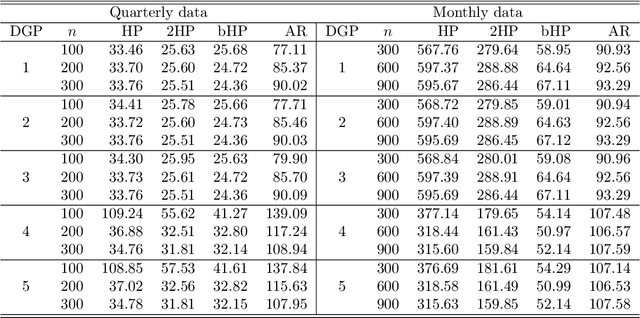
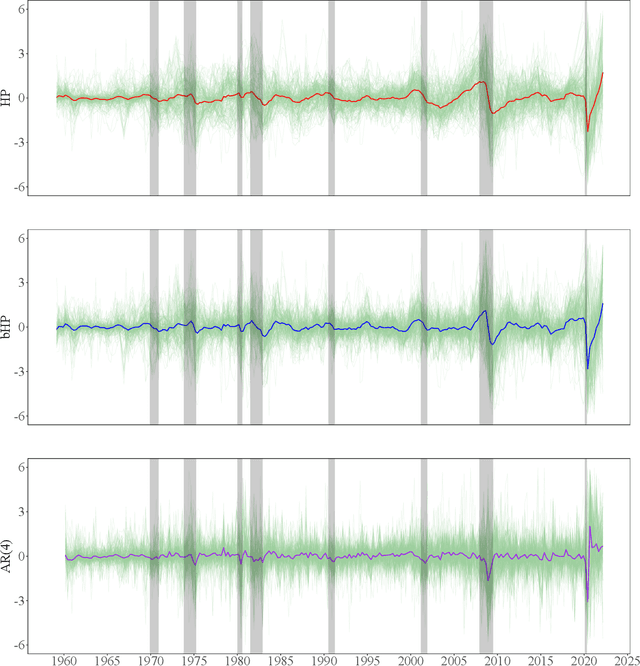
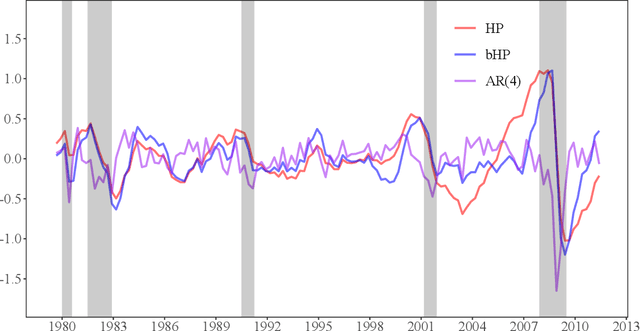
The global financial crisis and Covid recession have renewed discussion concerning trend-cycle discovery in macroeconomic data, and boosting has recently upgraded the popular HP filter to a modern machine learning device suited to data-rich and rapid computational environments. This paper sheds light on its versatility in trend-cycle determination, explaining in a simple manner both HP filter smoothing and the consistency delivered by boosting for general trend detection. Applied to a universe of time series in FRED databases, boosting outperforms other methods in timely capturing downturns at crises and recoveries that follow. With its wide applicability the boosted HP filter is a useful automated machine learning addition to the macroeconometric toolkit.

Boosting the Hodrick-Prescott Filter

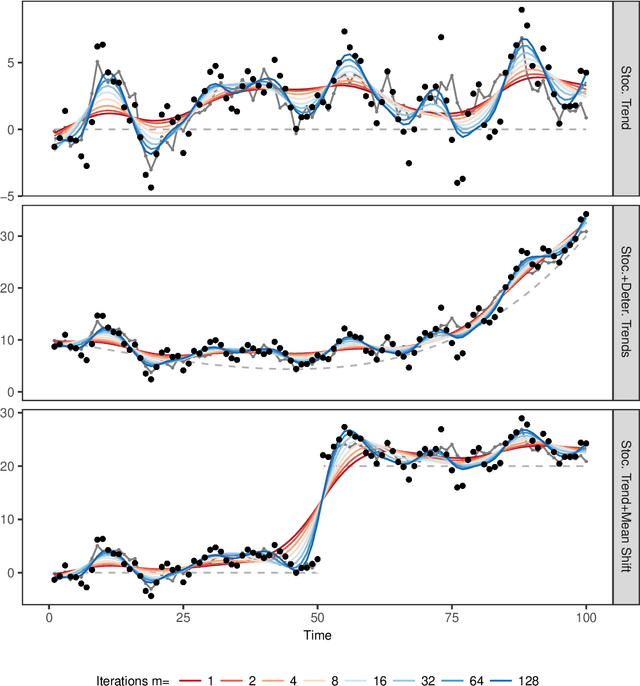
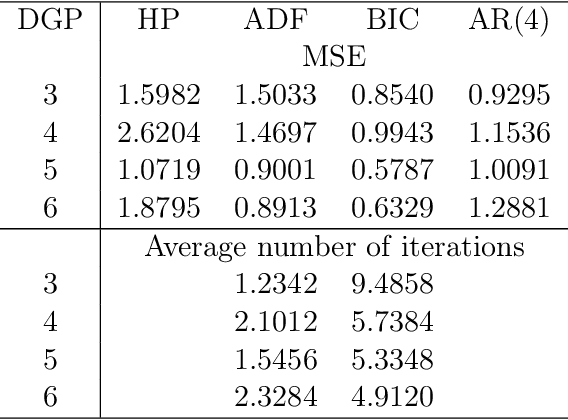
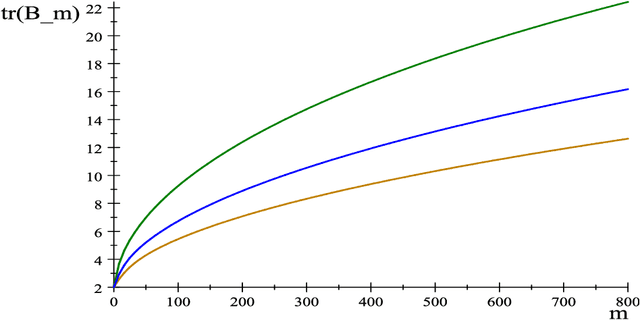
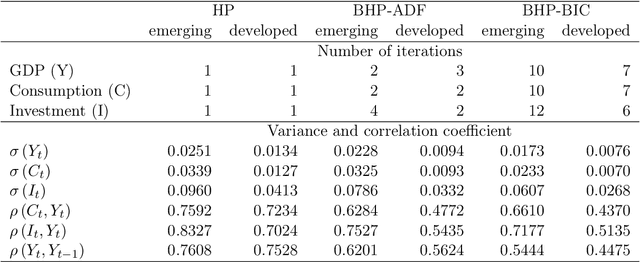
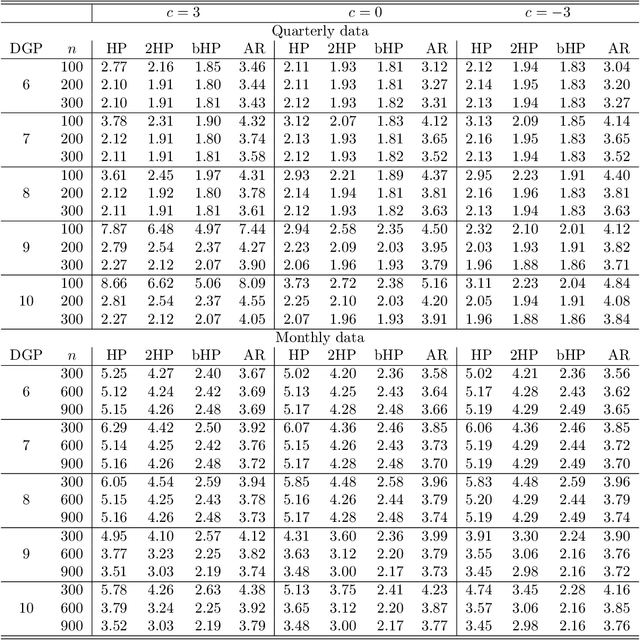
The Hodrick-Prescott (HP) filter is one of the most widely used econometric methods in applied macroeconomic research. The technique is nonparametric and seeks to decompose a time series into a trend and a cyclical component unaided by economic theory or prior trend specification. Like all nonparametric methods, the HP filter depends critically on a tuning parameter that controls the degree of smoothing. Yet in contrast to modern nonparametric methods and applied work with these procedures, empirical practice with the HP filter almost universally relies on standard settings for the tuning parameter that have been suggested largely by experimentation with macroeconomic data and heuristic reasoning about the form of economic cycles and trends. As recent research has shown, standard settings may not be adequate in removing trends, particularly stochastic trends, in economic data. This paper proposes an easy-to-implement practical procedure of iterating the HP smoother that is intended to make the filter a smarter smoothing device for trend estimation and trend elimination. We call this iterated HP technique the boosted HP filter in view of its connection to L2-boosting in machine learning. The paper develops limit theory to show that the boosted HP filter asymptotically recovers trend mechanisms that involve unit root processes, deterministic polynomial drifts, and polynomial drifts with structural breaks -- the most common trends that appear in macroeconomic data and current modeling methodology. A stopping criterion is used to automate the iterative HP algorithm, making it a data-determined method that is ready for modern data-rich environments in economic research. The methodology is illustrated using three real data examples that highlight the differences between simple HP filtering, the data-determined boosted filter, and an alternative autoregressive approach.