Differentiable Sparse Identification of Lagrangian Dynamics

Data-driven discovery of governing equations from data remains a fundamental challenge in nonlinear dynamics. Although sparse regression techniques have advanced system identification, they struggle with rational functions and noise sensitivity in complex mechanical systems. The Lagrangian formalism offers a promising alternative, as it typically avoids rational expressions and provides a more concise representation of system dynamics. However, existing Lagrangian identification methods are significantly affected by measurement noise and limited data availability. This paper presents a novel differentiable sparse identification framework that addresses these limitations through three key contributions: (1) the first integration of cubic B-Spline approximation into Lagrangian system identification, enabling accurate representation of complex nonlinearities, (2) a robust equation discovery mechanism that effectively utilizes measurements while incorporating known physical constraints, (3) a recursive derivative computation scheme based on B-spline basis functions, effectively constraining higher-order derivatives and reducing noise sensitivity on second-order dynamical systems. The proposed method demonstrates superior performance and enables more accurate and reliable extraction of physical laws from noisy data, particularly in complex mechanical systems compared to baseline methods.

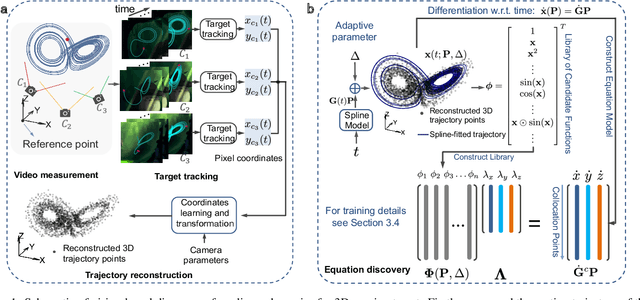
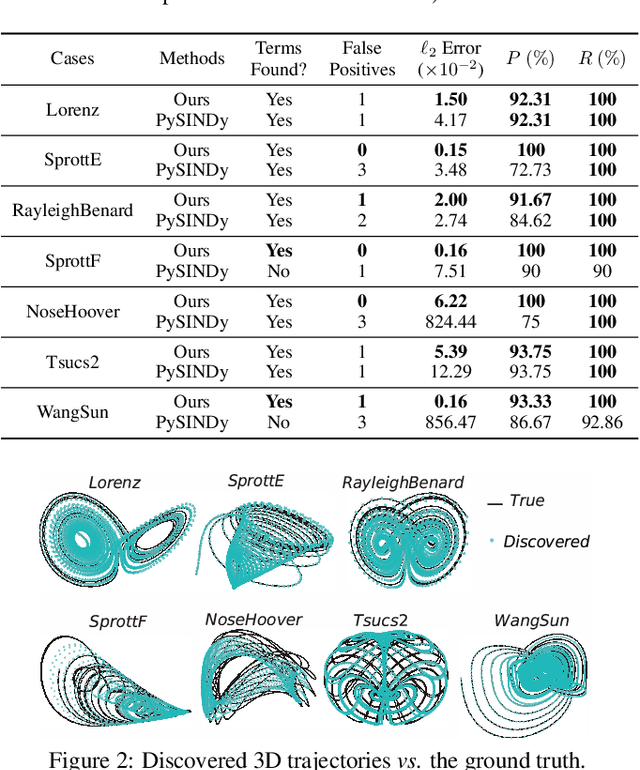
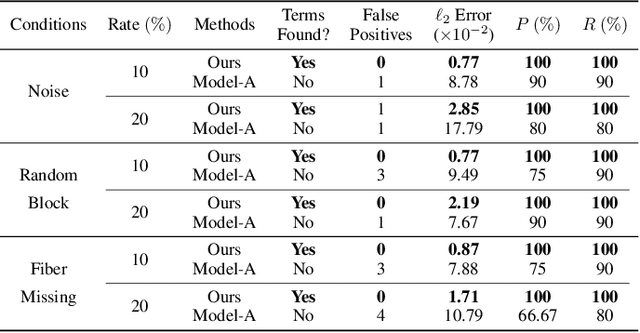
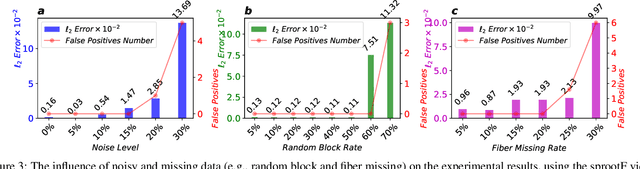
Vision-based Discovery of Nonlinear Dynamics for 3D Moving Target

Data-driven discovery of governing equations has kindled significant interests in many science and engineering areas. Existing studies primarily focus on uncovering equations that govern nonlinear dynamics based on direct measurement of the system states (e.g., trajectories). Limited efforts have been placed on distilling governing laws of dynamics directly from videos for moving targets in a 3D space. To this end, we propose a vision-based approach to automatically uncover governing equations of nonlinear dynamics for 3D moving targets via raw videos recorded by a set of cameras. The approach is composed of three key blocks: (1) a target tracking module that extracts plane pixel motions of the moving target in each video, (2) a Rodrigues' rotation formula-based coordinate transformation learning module that reconstructs the 3D coordinates with respect to a predefined reference point, and (3) a spline-enhanced library-based sparse regressor that uncovers the underlying governing law of dynamics. This framework is capable of effectively handling the challenges associated with measurement data, e.g., noise in the video, imprecise tracking of the target that causes data missing, etc. The efficacy of our method has been demonstrated through multiple sets of synthetic videos considering different nonlinear dynamics.

Solving the Travelling Thief Problem based on Item Selection Weight and Reverse Order Allocation

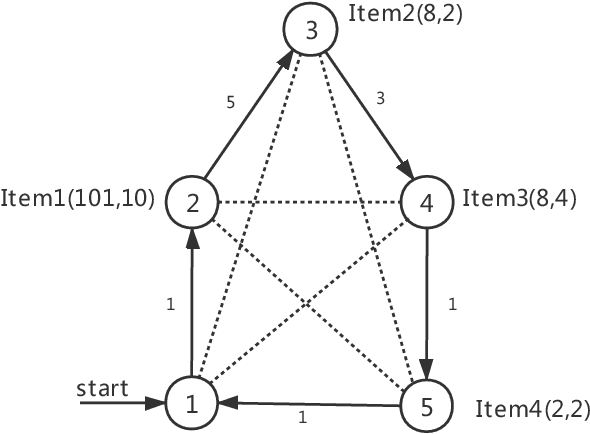
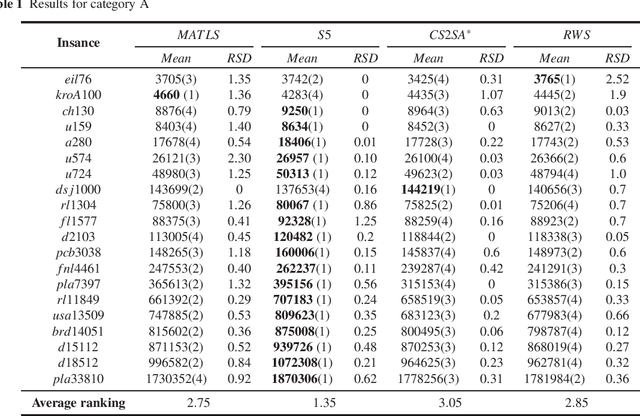
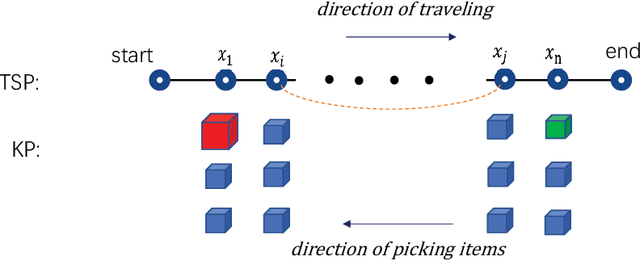
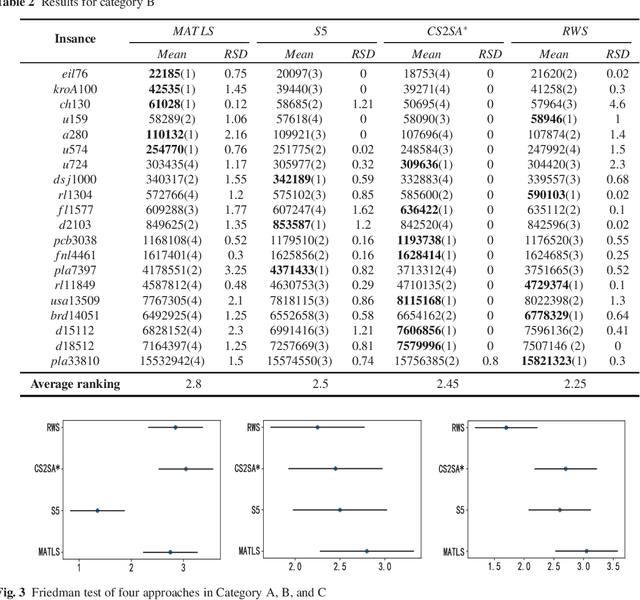
The Travelling Thief Problem (TTP) is a challenging combinatorial optimization problem that attracts many scholars. The TTP interconnects two well-known NP-hard problems: the Travelling Salesman Problem (TSP) and the 0-1 Knapsack Problem (KP). Increasingly algorithms have been proposed for solving this novel problem that combines two interdependent sub-problems. In this paper, TTP is investigated theoretically and empirically. An algorithm based on the score value calculated by our proposed formulation in picking items and sorting items in the reverse order in the light of the scoring value is proposed to solve the problem. Different approaches for solving the TTP are compared and analyzed; the experimental investigations suggest that our proposed approach is very efficient in meeting or beating current state-of-the-art heuristic solutions on a comprehensive set of benchmark TTP instances.