Zilong Tan
Model Reduction of Shallow CNN Model for Reliable Deployment of Information Extraction from Medical Reports
Jul 31, 2020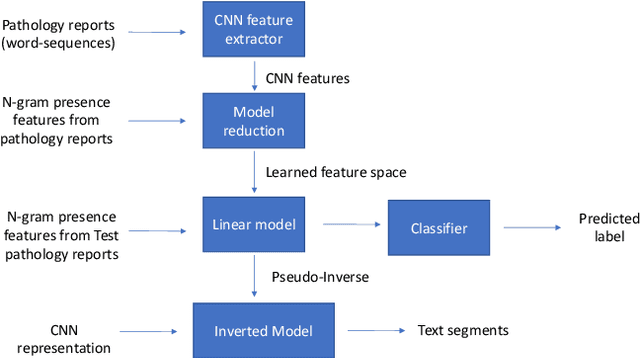

Abstract:Shallow Convolution Neural Network (CNN) is a time-tested tool for the information extraction from cancer pathology reports. Shallow CNN performs competitively on this task to other deep learning models including BERT, which holds the state-of-the-art for many NLP tasks. The main insight behind this eccentric phenomenon is that the information extraction from cancer pathology reports require only a small number of domain-specific text segments to perform the task, thus making the most of the texts and contexts excessive for the task. Shallow CNN model is well-suited to identify these key short text segments from the labeled training set; however, the identified text segments remain obscure to humans. In this study, we fill this gap by developing a model reduction tool to make a reliable connection between CNN filters and relevant text segments by discarding the spurious connections. We reduce the complexity of shallow CNN representation by approximating it with a linear transformation of n-gram presence representation with a non-negativity and sparsity prior on the transformation weights to obtain an interpretable model. Our approach bridge the gap between the conventionally perceived trade-off boundary between accuracy on the one side and explainability on the other by model reduction.
Learning Fair Representations for Kernel Models
Jun 27, 2019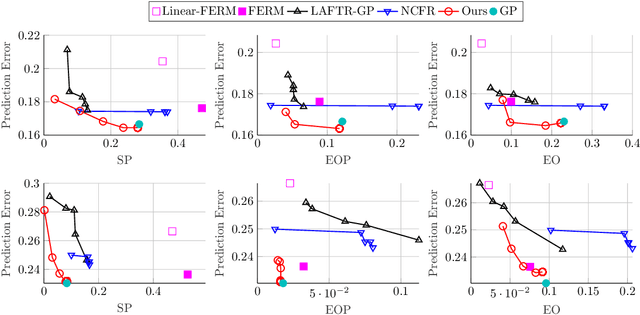
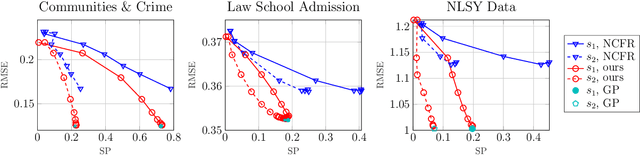
Abstract:Fair representations are a powerful tool for establishing criteria like statistical parity, proxy non-discrimination, and equality of opportunity in learned models. Existing techniques for learning these representations are typically model-agnostic, as they preprocess the original data such that the output satisfies some fairness criterion, and can be used with arbitrary learning methods. In contrast, we demonstrate the promise of learning a model-aware fair representation, focusing on kernel-based models. We leverage the classical Sufficient Dimension Reduction (SDR) framework to construct representations as subspaces of the reproducing kernel Hilbert space (RKHS), whose member functions are guaranteed to satisfy fairness. Our method supports several fairness criteria, continuous and discrete data, and multiple protected attributes. We further show how to calibrate the accuracy tradeoff by characterizing it in terms of the principal angles between subspaces of the RKHS. Finally, we apply our approach to obtain the first Fair Gaussian Process (FGP) prior for fair Bayesian learning, and show that it is competitive with, and in some cases outperforms, state-of-the-art methods on real data.
Subspace-Induced Gaussian Processes
Oct 06, 2018



Abstract:We present a dual formulation of the Gaussian process (GP) regression model using random functions in a reproducing kernel Hilbert space (RKHS). Compared to the GP, the proposed dual GP can realize an expanded space of functions for trace-class covariance kernels. In particular, the covariance of the dual GP is indexed or parameterized by a sufficient dimension reduction subspace of the RKHS, and will be low-rank while capturing the statistical dependency of the response on the covariates. This affords significant improvements in computational efficiency as well as potential reduction in the variance of predictions. We develop a fast Expectation-Maximization algorithm with improved computational complexity for estimating the parameters of the subspace-induced Gaussian process (SIGP). Extensive results on real-life data show that SIGP achieves competitive performance with a low-rank inducing subspace.
Scalable Algorithms for Learning High-Dimensional Linear Mixed Models
Mar 12, 2018



Abstract:Linear mixed models (LMMs) are used extensively to model dependecies of observations in linear regression and are used extensively in many application areas. Parameter estimation for LMMs can be computationally prohibitive on big data. State-of-the-art learning algorithms require computational complexity which depends at least linearly on the dimension $p$ of the covariates, and often use heuristics that do not offer theoretical guarantees. We present scalable algorithms for learning high-dimensional LMMs with sublinear computational complexity dependence on $p$. Key to our approach are novel dual estimators which use only kernel functions of the data, and fast computational techniques based on the subsampled randomized Hadamard transform. We provide theoretical guarantees for our learning algorithms, demonstrating the robustness of parameter estimation. Finally, we complement the theory with experiments on large synthetic and real data.
Efficient Learning of Mixed Membership Models
Jul 02, 2017

Abstract:We present an efficient algorithm for learning mixed membership models when the number of variables $p$ is much larger than the number of hidden components $k$. This algorithm reduces the computational complexity of state-of-the-art tensor methods, which require decomposing an $O\left(p^3\right)$ tensor, to factorizing $O\left(p/k\right)$ sub-tensors each of size $O\left(k^3\right)$. In addition, we address the issue of negative entries in the empirical method of moments based estimators. We provide sufficient conditions under which our approach has provable guarantees. Our approach obtains competitive empirical results on both simulated and real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge