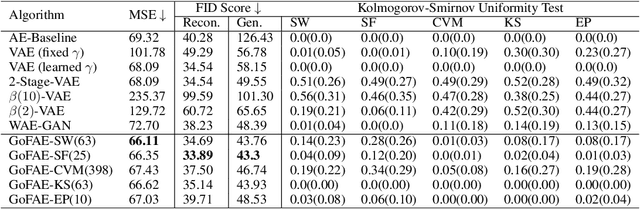
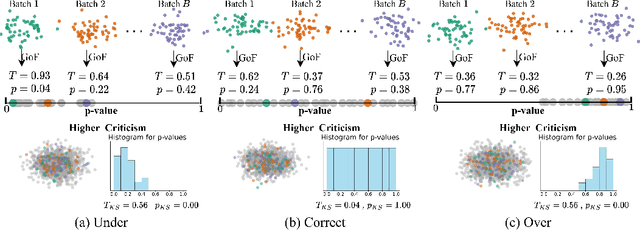
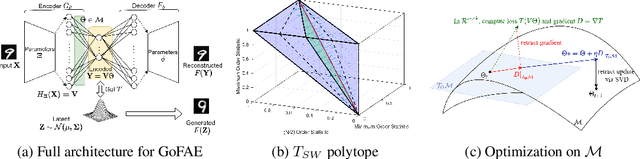
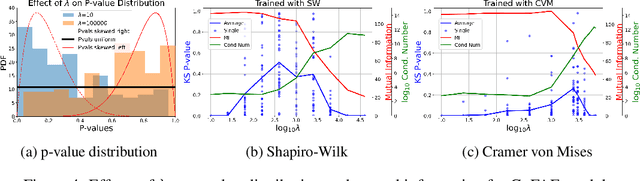
Auto-Encoding Goodness of Fit

For generative autoencoders to learn a meaningful latent representation for data generation, a careful balance must be achieved between reconstruction error and how close the distribution in the latent space is to the prior. However, this balance is challenging to achieve due to a lack of criteria that work both at the mini-batch (local) and aggregated posterior (global) level. Goodness of fit (GoF) hypothesis tests provide a measure of statistical indistinguishability between the latent distribution and a target distribution class. In this work, we develop the Goodness of Fit Autoencoder (GoFAE), which incorporates hypothesis tests at two levels. At the mini-batch level, it uses GoF test statistics as regularization objectives. At a more global level, it selects a regularization coefficient based on higher criticism, i.e., a test on the uniformity of the local GoF p-values. We justify the use of GoF tests by providing a relaxed $L_2$-Wasserstein bound on the distance between the latent distribution and target prior. We propose to use GoF tests and prove that optimization based on these tests can be done with stochastic gradient (SGD) descent on a compact Riemannian manifold. Empirically, we show that our higher criticism parameter selection procedure balances reconstruction and generation using mutual information and uniformity of p-values respectively. Finally, we show that GoFAE achieves comparable FID scores and mean squared errors with competing deep generative models while retaining statistical indistinguishability from Gaussian in the latent space based on a variety of hypothesis tests.

On $\ell_1$-regularized estimation for nonlinear models that have sparse underlying linear structures

In a recent work (arXiv:0910.2517), for nonlinear models with sparse underlying linear structures, we studied the error bounds of $\ell_0$-regularized estimation. In this note, we show that $\ell_1$-regularized estimation in some important cases can achieve the same order of error bounds as those in the aforementioned work.

$L_0$ regularized estimation for nonlinear models that have sparse underlying linear structures

We study the estimation of $\beta$ for the nonlinear model $y = f(X\sp{\top}\beta) + \epsilon$ when $f$ is a nonlinear transformation that is known, $\beta$ has sparse nonzero coordinates, and the number of observations can be much smaller than that of parameters ($n\ll p$). We show that in order to bound the $L_2$ error of the $L_0$ regularized estimator $\hat\beta$, i.e., $\|\hat\beta - \beta\|_2$, it is sufficient to establish two conditions. Based on this, we obtain bounds of the $L_2$ error for (1) $L_0$ regularized maximum likelihood estimation (MLE) for exponential linear models and (2) $L_0$ regularized least square (LS) regression for the more general case where $f$ is analytic. For the analytic case, we rely on power series expansion of $f$, which requires taking into account the singularities of $f$.

Estimators for Stochastic ``Unification-Based'' Grammars

Log-linear models provide a statistically sound framework for Stochastic ``Unification-Based'' Grammars (SUBGs) and stochastic versions of other kinds of grammars. We describe two computationally-tractable ways of estimating the parameters of such grammars from a training corpus of syntactic analyses, and apply these to estimate a stochastic version of Lexical-Functional Grammar.