Auto-Encoding Goodness of Fit
Paper and Code
Oct 12, 2022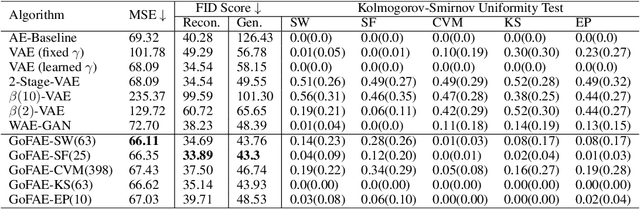
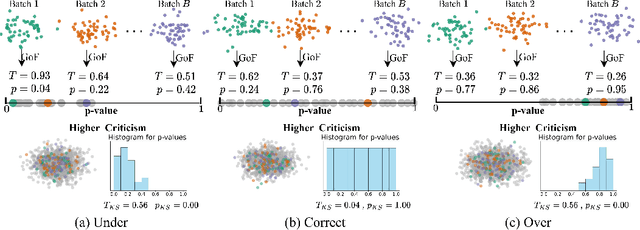
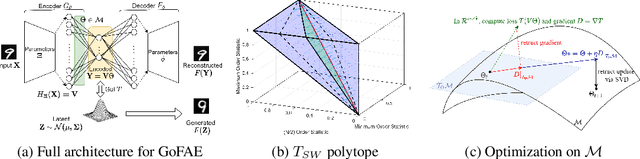
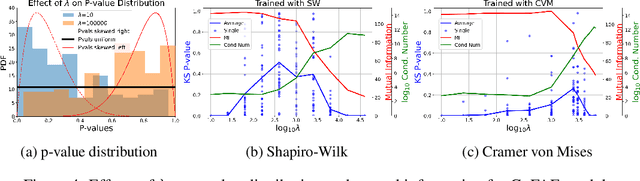
For generative autoencoders to learn a meaningful latent representation for data generation, a careful balance must be achieved between reconstruction error and how close the distribution in the latent space is to the prior. However, this balance is challenging to achieve due to a lack of criteria that work both at the mini-batch (local) and aggregated posterior (global) level. Goodness of fit (GoF) hypothesis tests provide a measure of statistical indistinguishability between the latent distribution and a target distribution class. In this work, we develop the Goodness of Fit Autoencoder (GoFAE), which incorporates hypothesis tests at two levels. At the mini-batch level, it uses GoF test statistics as regularization objectives. At a more global level, it selects a regularization coefficient based on higher criticism, i.e., a test on the uniformity of the local GoF p-values. We justify the use of GoF tests by providing a relaxed $L_2$-Wasserstein bound on the distance between the latent distribution and target prior. We propose to use GoF tests and prove that optimization based on these tests can be done with stochastic gradient (SGD) descent on a compact Riemannian manifold. Empirically, we show that our higher criticism parameter selection procedure balances reconstruction and generation using mutual information and uniformity of p-values respectively. Finally, we show that GoFAE achieves comparable FID scores and mean squared errors with competing deep generative models while retaining statistical indistinguishability from Gaussian in the latent space based on a variety of hypothesis tests.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge