Semi-supervised Regression Analysis with Model Misspecification and High-dimensional Data

The accessibility of vast volumes of unlabeled data has sparked growing interest in semi-supervised learning (SSL) and covariate shift transfer learning (CSTL). In this paper, we present an inference framework for estimating regression coefficients in conditional mean models within both SSL and CSTL settings, while allowing for the misspecification of conditional mean models. We develop an augmented inverse probability weighted (AIPW) method, employing regularized calibrated estimators for both propensity score (PS) and outcome regression (OR) nuisance models, with PS and OR models being sequentially dependent. We show that when the PS model is correctly specified, the proposed estimator achieves consistency, asymptotic normality, and valid confidence intervals, even with possible OR model misspecification and high-dimensional data. Moreover, by suppressing detailed technical choices, we demonstrate that previous methods can be unified within our AIPW framework. Our theoretical findings are verified through extensive simulation studies and a real-world data application.

On semi-supervised estimation using exponential tilt mixture models

Consider a semi-supervised setting with a labeled dataset of binary responses and predictors and an unlabeled dataset with only the predictors. Logistic regression is equivalent to an exponential tilt model in the labeled population. For semi-supervised estimation, we develop further analysis and understanding of a statistical approach using exponential tilt mixture (ETM) models and maximum nonparametric likelihood estimation, while allowing that the class proportions may differ between the unlabeled and labeled data. We derive asymptotic properties of ETM-based estimation and demonstrate improved efficiency over supervised logistic regression in a random sampling setup and an outcome-stratified sampling setup previously used. Moreover, we reconcile such efficiency improvement with the existing semiparametric efficiency theory when the class proportions in the unlabeled and labeled data are restricted to be the same. We also provide a simulation study to numerically illustrate our theoretical findings.

Persistently Trained, Diffusion-assisted Energy-based Models

Maximum likelihood (ML) learning for energy-based models (EBMs) is challenging, partly due to non-convergence of Markov chain Monte Carlo.Several variations of ML learning have been proposed, but existing methods all fail to achieve both post-training image generation and proper density estimation. We propose to introduce diffusion data and learn a joint EBM, called diffusion assisted-EBMs, through persistent training (i.e., using persistent contrastive divergence) with an enhanced sampling algorithm to properly sample from complex, multimodal distributions. We present results from a 2D illustrative experiment and image experiments and demonstrate that, for the first time for image data, persistently trained EBMs can {\it simultaneously} achieve long-run stability, post-training image generation, and superior out-of-distribution detection.

Understanding Accelerated Gradient Methods: Lyapunov Analyses and Hamiltonian Assisted Interpretations

We formulate two classes of first-order algorithms more general than previously studied for minimizing smooth and strongly convex or, respectively, smooth and convex functions. We establish sufficient conditions, via new discrete Lyapunov analyses, for achieving accelerated convergence rates which match Nesterov's methods in the strongly and general convex settings. Next, we study the convergence of limiting ordinary differential equations (ODEs) and point out currently notable gaps between the convergence properties of the corresponding algorithms and ODEs. Finally, we propose a novel class of discrete algorithms, called the Hamiltonian assisted gradient method, directly based on a Hamiltonian function and several interpretable operations, and then demonstrate meaningful and unified interpretations of our acceleration conditions.

Tractable and Near-Optimal Adversarial Algorithms for Robust Estimation in Contaminated Gaussian Models

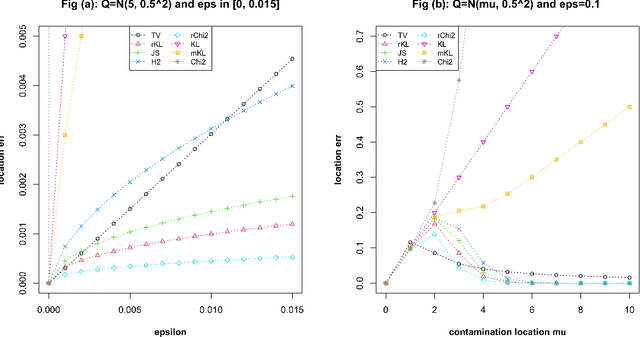
Consider the problem of simultaneous estimation of location and variance matrix under Huber's contaminated Gaussian model. First, we study minimum $f$-divergence estimation at the population level, corresponding to a generative adversarial method with a nonparametric discriminator and establish conditions on $f$-divergences which lead to robust estimation, similarly to robustness of minimum distance estimation. More importantly, we develop tractable adversarial algorithms with simple spline discriminators, which can be implemented via nested optimization such that the discriminator parameters can be fully updated by maximizing a concave objective function given the current generator. The proposed methods are shown to achieve minimax optimal rates or near-optimal rates depending on the $f$-divergence and the penalty used. We present simulation studies to demonstrate advantages of the proposed methods over classic robust estimators, pairwise methods, and a generative adversarial method with neural network discriminators.

Semi-supervised Logistic Learning Based on Exponential Tilt Mixture Models

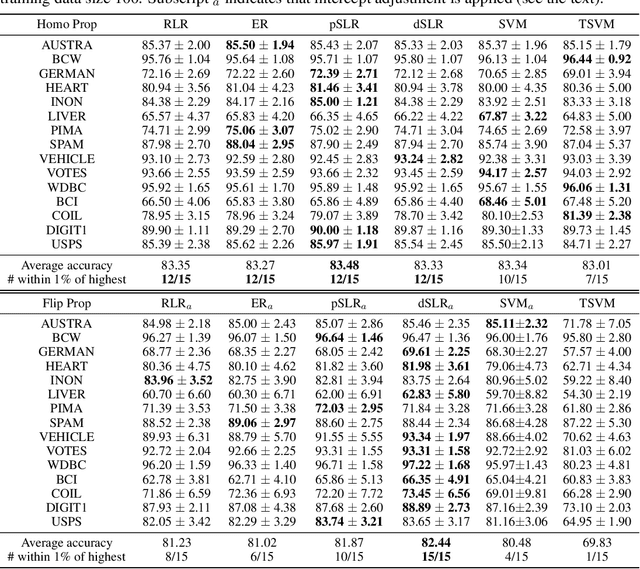
Consider semi-supervised learning for classification, where both labeled and unlabeled data are available for training. The goal is to exploit both datasets to achieve higher prediction accuracy than just using labeled data alone. We develop a semi-supervised logistic learning method based on exponential tilt mixture models, by extending a statistical equivalence between logistic regression and exponential tilt modeling. We study maximum nonparametric likelihood estimation and derive novel objective functions which are shown to be Fisher consistent. We also propose regularized estimation and construct simple and highly interpretable EM algorithms. Finally, we present numerical results which demonstrate the advantage of the proposed methods compared with existing methods.