Tractable and Near-Optimal Adversarial Algorithms for Robust Estimation in Contaminated Gaussian Models
Paper and Code
Dec 24, 2021

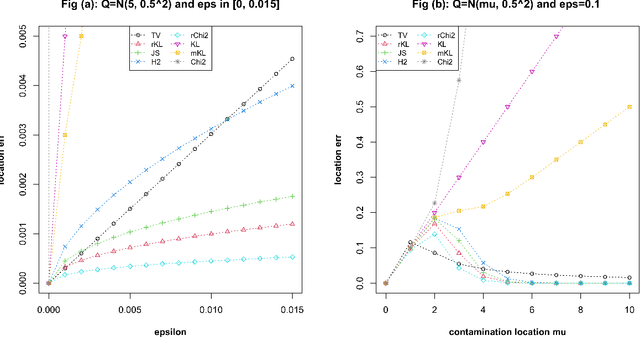

Consider the problem of simultaneous estimation of location and variance matrix under Huber's contaminated Gaussian model. First, we study minimum $f$-divergence estimation at the population level, corresponding to a generative adversarial method with a nonparametric discriminator and establish conditions on $f$-divergences which lead to robust estimation, similarly to robustness of minimum distance estimation. More importantly, we develop tractable adversarial algorithms with simple spline discriminators, which can be implemented via nested optimization such that the discriminator parameters can be fully updated by maximizing a concave objective function given the current generator. The proposed methods are shown to achieve minimax optimal rates or near-optimal rates depending on the $f$-divergence and the penalty used. We present simulation studies to demonstrate advantages of the proposed methods over classic robust estimators, pairwise methods, and a generative adversarial method with neural network discriminators.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge