High Confidence Level Inference is Almost Free using Parallel Stochastic Optimization

Uncertainty quantification for estimation through stochastic optimization solutions in an online setting has gained popularity recently. This paper introduces a novel inference method focused on constructing confidence intervals with efficient computation and fast convergence to the nominal level. Specifically, we propose to use a small number of independent multi-runs to acquire distribution information and construct a t-based confidence interval. Our method requires minimal additional computation and memory beyond the standard updating of estimates, making the inference process almost cost-free. We provide a rigorous theoretical guarantee for the confidence interval, demonstrating that the coverage is approximately exact with an explicit convergence rate and allowing for high confidence level inference. In particular, a new Gaussian approximation result is developed for the online estimators to characterize the coverage properties of our confidence intervals in terms of relative errors. Additionally, our method also allows for leveraging parallel computing to further accelerate calculations using multiple cores. It is easy to implement and can be integrated with existing stochastic algorithms without the need for complicated modifications.

Spectral Ranking Inferences based on General Multiway Comparisons

This paper studies the performance of the spectral method in the estimation and uncertainty quantification of the unobserved preference scores of compared entities in a very general and more realistic setup in which the comparison graph consists of hyper-edges of possible heterogeneous sizes and the number of comparisons can be as low as one for a given hyper-edge. Such a setting is pervasive in real applications, circumventing the need to specify the graph randomness and the restrictive homogeneous sampling assumption imposed in the commonly-used Bradley-Terry-Luce (BTL) or Plackett-Luce (PL) models. Furthermore, in the scenarios when the BTL or PL models are appropriate, we unravel the relationship between the spectral estimator and the Maximum Likelihood Estimator (MLE). We discover that a two-step spectral method, where we apply the optimal weighting estimated from the equal weighting vanilla spectral method, can achieve the same asymptotic efficiency as the MLE. Given the asymptotic distributions of the estimated preference scores, we also introduce a comprehensive framework to carry out both one-sample and two-sample ranking inferences, applicable to both fixed and random graph settings. It is noteworthy that it is the first time effective two-sample rank testing methods are proposed. Finally, we substantiate our findings via comprehensive numerical simulations and subsequently apply our developed methodologies to perform statistical inferences on statistics journals and movie rankings.

Communication-Efficient Distributed Estimation and Inference for Cox's Model

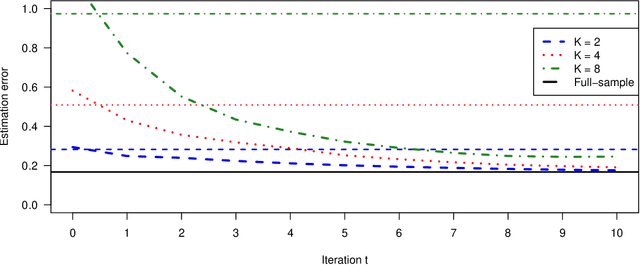
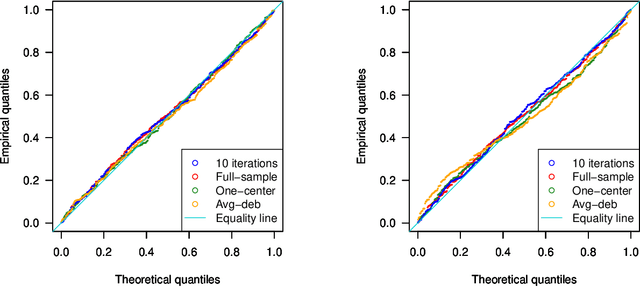
Motivated by multi-center biomedical studies that cannot share individual data due to privacy and ownership concerns, we develop communication-efficient iterative distributed algorithms for estimation and inference in the high-dimensional sparse Cox proportional hazards model. We demonstrate that our estimator, even with a relatively small number of iterations, achieves the same convergence rate as the ideal full-sample estimator under very mild conditions. To construct confidence intervals for linear combinations of high-dimensional hazard regression coefficients, we introduce a novel debiased method, establish central limit theorems, and provide consistent variance estimators that yield asymptotically valid distributed confidence intervals. In addition, we provide valid and powerful distributed hypothesis tests for any coordinate element based on a decorrelated score test. We allow time-dependent covariates as well as censored survival times. Extensive numerical experiments on both simulated and real data lend further support to our theory and demonstrate that our communication-efficient distributed estimators, confidence intervals, and hypothesis tests improve upon alternative methods.

Ranking Inferences Based on the Top Choice of Multiway Comparisons

This paper considers ranking inference of $n$ items based on the observed data on the top choice among $M$ randomly selected items at each trial. This is a useful modification of the Plackett-Luce model for $M$-way ranking with only the top choice observed and is an extension of the celebrated Bradley-Terry-Luce model that corresponds to $M=2$. Under a uniform sampling scheme in which any $M$ distinguished items are selected for comparisons with probability $p$ and the selected $M$ items are compared $L$ times with multinomial outcomes, we establish the statistical rates of convergence for underlying $n$ preference scores using both $\ell_2$-norm and $\ell_\infty$-norm, with the minimum sampling complexity. In addition, we establish the asymptotic normality of the maximum likelihood estimator that allows us to construct confidence intervals for the underlying scores. Furthermore, we propose a novel inference framework for ranking items through a sophisticated maximum pairwise difference statistic whose distribution is estimated via a valid Gaussian multiplier bootstrap. The estimated distribution is then used to construct simultaneous confidence intervals for the differences in the preference scores and the ranks of individual items. They also enable us to address various inference questions on the ranks of these items. Extensive simulation studies lend further support to our theoretical results. A real data application illustrates the usefulness of the proposed methods convincingly.

Robust High-dimensional Tuning Free Multiple Testing

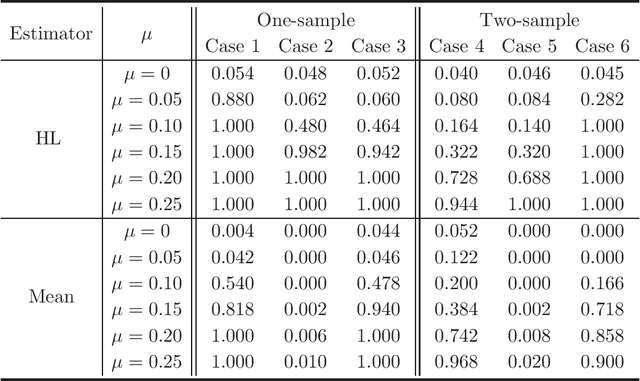
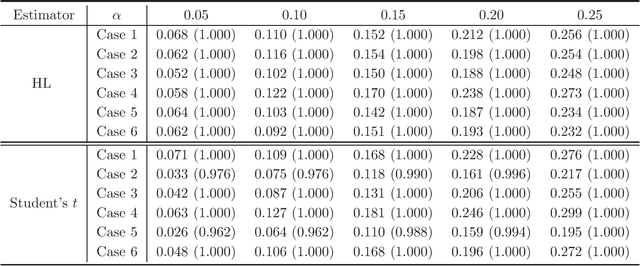
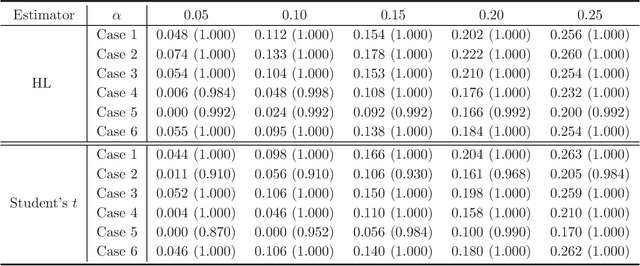
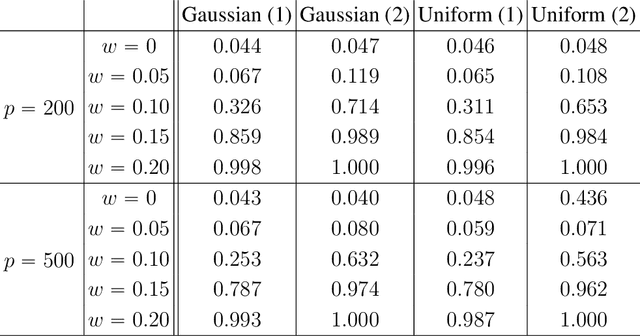
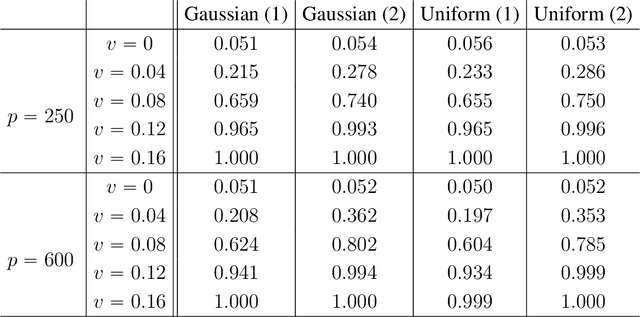
A stylized feature of high-dimensional data is that many variables have heavy tails, and robust statistical inference is critical for valid large-scale statistical inference. Yet, the existing developments such as Winsorization, Huberization and median of means require the bounded second moments and involve variable-dependent tuning parameters, which hamper their fidelity in applications to large-scale problems. To liberate these constraints, this paper revisits the celebrated Hodges-Lehmann (HL) estimator for estimating location parameters in both the one- and two-sample problems, from a non-asymptotic perspective. Our study develops Berry-Esseen inequality and Cram\'{e}r type moderate deviation for the HL estimator based on newly developed non-asymptotic Bahadur representation, and builds data-driven confidence intervals via a weighted bootstrap approach. These results allow us to extend the HL estimator to large-scale studies and propose \emph{tuning-free} and \emph{moment-free} high-dimensional inference procedures for testing global null and for large-scale multiple testing with false discovery proportion control. It is convincingly shown that the resulting tuning-free and moment-free methods control false discovery proportion at a prescribed level. The simulation studies lend further support to our developed theory.

Are Latent Factor Regression and Sparse Regression Adequate?

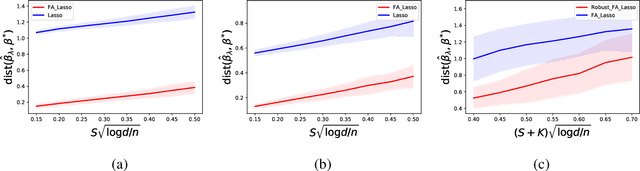
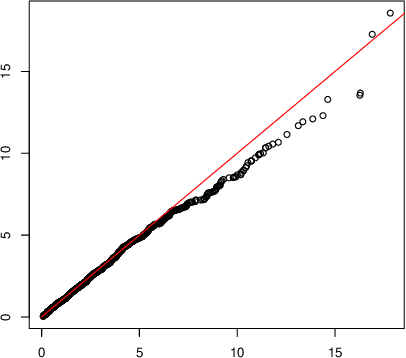
We propose the Factor Augmented sparse linear Regression Model (FARM) that not only encompasses both the latent factor regression and sparse linear regression as special cases but also bridges dimension reduction and sparse regression together. We provide theoretical guarantees for the estimation of our model under the existence of sub-Gaussian and heavy-tailed noises (with bounded (1+x)-th moment, for all x>0), respectively. In addition, the existing works on supervised learning often assume the latent factor regression or the sparse linear regression is the true underlying model without justifying its adequacy. To fill in such an important gap, we also leverage our model as the alternative model to test the sufficiency of the latent factor regression and the sparse linear regression models. To accomplish these goals, we propose the Factor-Adjusted de-Biased Test (FabTest) and a two-stage ANOVA type test respectively. We also conduct large-scale numerical experiments including both synthetic and FRED macroeconomics data to corroborate the theoretical properties of our methods. Numerical results illustrate the robustness and effectiveness of our model against latent factor regression and sparse linear regression models.